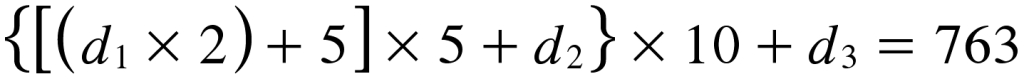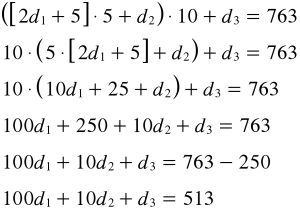Brincadeira #1. “Escolha um algarismo de 0 a 9”, diz o adulto à criança em idade escolar.
“Escolho o 6.”
O adulto pensa um pouco e anota na lousa: 68.
“Escola outro algarismo de 0 a 9.”
“Escolho o 5.”
O adulto pensa mais um tempo, como se estivesse resolvendo um problema difícil, e anota na lousa: 6851.
“Você escolheu dois algarismos, e eu escolhi outros dois, com base nos algarismos que você escolheu. Digo agora que, se você formar um outro número com os algarismos de 6851, e se tirar esse número de 6851, o resultado é divisível por 9.”
A criança pega 6851 e forma 1685, e usa a calculadora do celular para calcular 6.851 – 1.685 = 5.166, e então divide 5.166 por 9 para obter 574.
“É verdade!”, ela diz com assombro. “Como você fez isso?”
“Eu tenho meus truques.”
* * *
Pegue um inteiro não negativo x qualquer, grafado no sistema posicional decimal comum. Pegue qualquer inteiro y que possa montar com uma permutação dos algarismos de x. Considere o valor absoluto da diferença entre x e y, isto é, faça x – y se x > y ou y – x se y > x.
Problema 1. Veja se identifica algum padrão e formule uma hipótese a respeito dele.
* * *
Por exemplo, o inteiro 231.
231 – 231 = 0 ;
231 – 213 = 18 = 2 · 32 ;
231 – 123 = 108 = 22 · 33 ;
231 – 132 = 99 = 32 · 11 ;
321 – 231 = 90 = 2 · 32 · 5 ;
312 – 231 = 81 = 34
Se fizer isso com vários inteiros, cedo ou tarde vai chegar à seguinte hipótese: sempre é o caso de que 32 é fator de |x – y|. Reescrevendo o exemplo de 231 à luz da hipótese:
231 – 231 = 0 · 32 ;
231 – 213 = 18 = 2 · 32 ;
231 – 123 = 108 = 22 · 32 · 3 ;
231 – 132 = 99 = 32 · 11 ;
321 – 231 = 90 = 2 · 32 · 5 ;
312 – 231 = 81 = 32 · 32
Ou então, melhor dizendo:
Hipótese H1. Considere o inteiro não negativo x, grafado no sistema posicional decimal hindu-arábico. Subtraia de x qualquer inteiro y que possa formar com uma permutação dos algarismos de x, e calcule o valor absoluto |x – y| da diferença entre x e y. Daí 9 divide |x – y|, isto é, 32 é um dos fatores de |x – y|.
Professores experientes dizem que sempre há um aluno (ou aluna) que levanta essa hipótese, tanto no ensino fundamental quanto no médio.
Problema 2. Como pode provar a hipótese? (Dica: use a aritmética ao módulo 9.)
Problema 3. Como pode se preparar para ajudar o aluno, que não tem as mesmas ferramentas teóricas que você, a provar a hipótese com as ferramentas que ele tem?
* * *
Resolução do problema 2. Na postagem Álgebra Abstrata: Um Amor à Primeira Vista, você encontra os elementos teóricos para montar uma resolução como a que verá em seguida. Importante: note que, ao módulo 9, [10n] = [1], expressão na qual n é um inteiro não negativo. (Lembrete: nesta postagem, [x] denota o conjunto de inteiros congruentes a x (mod 9), isto é, [x] = {y : y ∈ ℤ ∧ y ≡ x (mod 9).)
Prova da hipótese H1. Faça x um inteiro não negativo qualquer. Faça drdr–1dr–2…d1d0 a representação decimal de x. Por exemplo, se x é o inteiro 9.745, daí d3 = 9, d2 = 7, d1 = 4, e d0 = 5 e, além disso, x = 9 · 103 + 7 · 102 + 4 · 101 + 5 · 100.
Pensando sempre assim, a linha a seguir é verdadeira.
x = dr · 10r + dr–1 · 10r–1 + dr–2 · 10r–2 + ··· + d1 · 10 + d0
Mas daí, sempre ao módulo 9:
[x] = [dr · 10r + dr–1 · 10r–1 + dr–2 · 10r–2 + ··· + d1 · 10 + d0]
= [dr · 10r] + [dr–1 · 10r–1] + [dr–2 · 10r–2] + ··· + [d1 · 10] + [d0]
= [[dr] · [10r]] + [[dr–1] · [10r–1]] + [[dr–2] · [10r–2]] + ··· + [[d1] · [10]] + [d0]
= [[dr] · [1]] + [[dr–1] · [1]] + [[dr–2] · [1]] + ··· + [[d1] · [1]] + [d0]
= [dr] + [dr–1] + [dr–2] + ··· + [d1] + [d0]
= [dr + dr–1 + dr–2 + ··· + d1 + d0]
∴ x ≡ dr + dr–1 + dr–2 + ··· + d1 + d0 (mod 9)
Essa última linha diz que todo inteiro, grafado na notação posicional decimal, é congruente (mod 9) com a soma de seus algarismos.
Faça agora y um algarismo que vai montar com uma permutação dos algarismos de x. Daí dirdir–1dir–2…di1di0 é a representação decimal de y, na qual dir, dir–1, dir–2, …, di1, di0 é uma das permutações dos algarismos de x. Usando o mesmo argumento logo acima, mutatis mutandis:
y ≡ dir + dir–1 + dir–2 + ··· + di1 + di0 (mod 9)
Em palavras, y é congruente com a soma da permutação dos dígitos de x. Contudo, vale lembrar que a adição é comutativa (a ordem das parcelas não altera a soma), e portanto, ao módulo 9:
[x] = [y] ;
[x – y] = [dr + dr–1 + dr–2 + ··· + d1 + d0] – [dir + dir–1 + dir–2 + ··· + di1 + di0] ;
[x – y] = [0] ;
∴ x – y ≡ 0 (mod 9)
E essa última linha prova a hipótese H1: 9 divide |x – y|, isto é, 32 é um dos fatores de |x – y|.
* * *
Resolução do problema 3. O problema 3 é mais difícil que o 2. Provar a hipótese H1 sem as ferramentas da aritmética ao módulo m requer do estudante uma boa dose de astúcia.
Um jeito de começar é pedir para o estudante provar o seguinte: Um inteiro não negativo é divisível por 9 se-se a soma de seus algarismos é divisível por 9.
O primeiro passo é notar que, quando o estudante divide uma potência de 10 por 9, o resto é sempre igual a 1. Por exemplo, 100.000 = (11.111 · 9) + 1. Isso porque 100.000 – 1 = 99.999 = 11.111 · 9. Em geral:
10n = (111···1 · 9) + 1
Expressão na qual 111···1 tem n algarismos iguais a 1. Veja como usar esse fato na prova de que 243 é divisível por 9:
243 = 2 · 100 + 4 · 10 + 3
Substitua as potências de 10.
243 = 2 · (11 · 9 + 1) + 4 · (1 · 9 + 1) + 3
Use a propriedade distributiva da multiplicação sobre a adição.
243 = (2 · 11 · 9 + 2) + (4 · 9 + 4) + 3
Use as propriedades comutativa e associativa da adição para reorganizar os termos à direita da igualdade, com os termos claramente divisíveis por 9 reunidos numa parcela, e os outros termos reunidos em outra.
243 = (2 · 11 · 9 + 4 · 9) + (2 + 4 + 3)
Visto que 9 divide a primeira parcela (2 · 11 · 9 + 4 · 9), daí, se 9 também divide 243, então obrigatoriamente 9 divide a parcela (2 + 4 + 3), isto é, 9 tem de dividir a soma dos algarismos de 243. Da mesma forma, visto que 9 divide a primeira parcela (2 · 11 · 9 + 4 · 9) e também divide a parcela (2 + 4 + 3), então obrigatoriamente 9 divide o número 243.
Depois de repetir essa prova para alguns inteiros divisíveis por 9 (ou não), o estudante pode generalizá-la para um inteiro x com 4 algarismos, por exemplo o inteiro d3d2d1d0, em que d3, d2, d1, d0 são algarismos ou dígitos de 0 a 9.
x = d3 · 103 + d2 · 102 + d1 · 10 + d0
Substitua as potências de 10.
x = d3 · (111 · 9 + 1) + d2 · (11 · 9 + 1) + d1 · (1 · 9 + 1) + d0
Use a propriedade distributiva da multiplicação sobre a adição.
x = 111 · 9 · d3 + d3 + 11 · 9 · d2 + d2 + 1 · 9 · d1 + d1 + d0
Use as propriedades comutativa e associativa da adição para reorganizar os termos à direita da igualdade, com os termos claramente divisíveis por 9 reunidos numa parcela, e os outros termos reunidos em outra.
x = (111 · 9 · d3 + 11 · 9 · d2 + 1 · 9 · d1) + (d3 + d2 + d1 + d0)
Visto que 9 divide a primeira parcela (111 · 9 · d3 + 11 · 9 · d2 + 1 · 9 · d1), daí, se 9 também divide x, então obrigatoriamente 9 divide a segunda parcela (d3 + d2 + d1 + d0), isto é, 9 divide a soma dos algarismos de x — e vice-versa, mutatis mutandis.
A partir desse ponto, o estudante está pronto para generalizar essa prova para um inteiro não negativo com número não especificado de algarismos. Por último, usando a propriedade comutativa da adição, ele tem condições de provar a hipótese H1.
* * *
Brincadeira #2. “Escolha num número de 0 a 100”, diz o adulto à criança em idade escolar.
“Escolhi!”
“Me diga qual é.”
“Escolhi o 77.”
O adulto fica pensando um tempão, fazendo o maior teatro, como se fosse o gênio dos gênios.
“Coloque três zeros antes de 77.”
“Entendi: 00077.”
“Sim. Agora, embaralhe os algarismos de 00077 para formar um novo número.”
“Pode ser 70007?”
“Pode. Tire o número que você pensou primeiro, o 77, de 70007, que o resultado da subtração é divisível por 9.”
“Como você sabe?”
“Eu tenho meus truques.”
A criança pega o celular, ativa a calculadora, calcula 70.007 – 77 = 69.930, e depois divide 69.930 por 9, o que dá 7.770.
“É verdade!”
Brincadeira #3. “Pense num número, mas não me diga qual é.” O adulto fica olhando o rosto da criança com tremenda intensidade.
“Pronto!” A criança pensou em 6.906.
“Quantos algarismos tem o seu número?”
“Tem quatro.”
O adulto pensa um tempão, fazendo o maior teatro, examinando de vez em quando o rosto da criança.
“Então coloque o algarismo 1 entre o primeiro e o segundo algarismo, coloque os algarismos 22 entre o segundo e o terceiro, e coloque os algarismos 333 entre o terceiro e o quarto. Pode anotar num papel, se quiser, mas não mostre para mim.”
A criança anota 6192203336.
“Agora forme um número com uma permutação dos algarismos do número que você anotou no papel.”
A criança forma, por exemplo, 1263239063.
“Agora tire um número do outro. Pode tirar o menor do maior. Digo que o resultado é divisível por 9.”
A criança usa o celular para calcular 6.192.203.336 – 1.263.239.063 = 4.928.964.273, e depois divide 4.928.964.273 por 9 para obter 547.662.697.
“É verdade! Como você fez isso?”
“Eu tenho meus truques. O segredo é saber quais algarismos adicionar entre os algarismos do número que você pensou, conforme o número de algarismos do número que você pensou, e conforme também o movimento dos seus olhos.”
Essa última frase é falsa, mas um truque de mágica é, como o nome diz, pura traquinagem. {FIM}
Observações:
1. Esta é a última postagem deste ano. Desejo a todos a capacidade de tomar decisões sábias em 2022, por meio das quais o Brasil se transforme num país mais civilizado e justo.
2. Visto que, ao módulo 3, [10n] = [1], com n inteiro não negativo, você pode facilmente adaptar o conteúdo desta postagem para a divisão por 3. Mais especificamente, e sempre pensando em inteiros não negativos grafados com o sistema posicional decimal: (a) Um número é divisível por 3 se-se a soma de seus algarismos é divisível por 3; (b) Forme um número y a partir da permutação dos algarismos de um certo número x, e daí |x – y| é divisível por 3.
3. Há uma postagem mais completa sobre esse assunto, a divisão por 9, e sobre esse mesmo assunto generalizado para outras bases além da base 10: Uma Beleza: Quando 9 Divide um Inteiro.
4. Com um ábaco aberto, é fácil mostrar que 10n = 999···9 + 1, expressão na qual 999···9 tem n algarismos iguais a 9. Começando com o ábaco vazio, ponha, por exemplo, uma argola no pino M dos milhares. Isso representa o número 1.000. Você tem três pinos vazios à direita do pino M, que são os pinos C, D, U das centenas, dezenas, e unidades. Troque uma argola no pino M por dez argolas no pino C. Troque uma argola no pino C por dez argolas no pino D. Troque uma argola no pino D por dez argolas no pino U. Por fim, subtraia uma argola no pino U. Vai ficar com nove argolas no pino C, nove argolas no pino D, e nove argolas no pino U; ou, dizendo de outro modo, esse procedimento mostra claramente que 103 = 999 + 1.