Pode existir um mapa da Inglaterra perfeitamente completo? Tão completo que, no próprio mapa, há um mapa do mapa? Tão completo que, no mapa do mapa, há um mapa do mapa do mapa? Tão completo que, no mapa do mapa … do mapa (n vezes), há um mapa do mapa … do mapa (n + 1 vezes) — e assim por diante ao infinito?
Quem fez a si mesmo essa pergunta foi o filósofo americano Josiah Royce. Ela está no livro The World and the Individual [O Mundo e o Indivíduo], de 1898. Por exemplo, neste trecho:
Qualquer que seja nossa teoria a respeito do significado dos verbos ser e existir, suponha que alguém […] nos garantisse a verdade da afirmação a seguir, qual seja: “Aberto sobre a superfície da Inglaterra, e portanto aberto dentro do território inglês, existe de alguma forma um mapa absolutamente perfeito de toda a Inglaterra — não interessa aqui como foi feito, nem quando.” Suponha que já aceitamos essa afirmação como sendo verdadeira. Daí em algum momento tentamos descobrir o significado implícito nessa afirmação. Devemos de imediato observar que a afirmação a seguir, “Uma parte da Inglaterra mapeia perfeitamente a Inglaterra inteira, mas numa escala menor”, nos diz algo não sobre o processo de desenhar mapas, mas sim sobre a coexistente presença, na Inglaterra, de um número infinito de mapas, mapas tais como foram descritos. Estaríamos afirmando a série infinita inteira, que não possui um último termo, como sendo um fato da existência. O mapa absolutamente perfeito da Inglaterra, repousado aberto sobre uma parte do território inglês, se realmente foi executado à perfeição, contém necessariamente em sua estrutura uma série de mapas dentro de mapas tais que nenhum dos mapas pode ser o último da série.
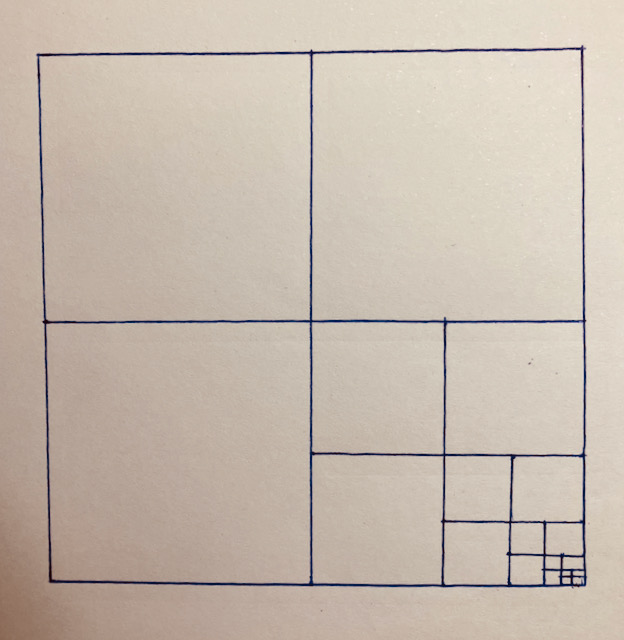
Há um jeito simples de visualizar o que Royce está dizendo: imagine que a Inglaterra é um quadrado dividido em quatro partes iguais por uma cruz, isto é, uma linha vertical e outra linha horizontal. Assim:
Use o quadrado inferior direito para colocar, aberto, o mapa perfeito da Inglaterra.
Mas, se esse mapa é absolutamente perfeito, então contém um segundo mapa dentro do primeiro mapa, um terceiro mapa dentro do segundo mapa, um quarto mapa dentro do terceiro mapa, e assim por diante. Eis as regras desse objeto abstrato recursivo:
Regra inicial. O primeiro mapa M0 é um quadrado dividido em quatro quadrados iguais por duas semirretas em cruz.
Regra de sucessão. Para qualquer n, o mapa sucessor Mn+1 é igual ao mapa Mn, mas com o quadrado inferior direito dividido em quatro quadrados iguais por meio de duas semirretas em cruz.
Regra de limite. O mapa-limite Mω é a sobreposição dos mapas Mn para todo n inteiro não negativo.
Na figura a seguir, veja as primeiras seis iterações deste mapa de Royce.
Royce propôs tais objetos abstratos (que hoje se chamam “mapas de Royce”) porque estava preocupado com teologia. Queria tornar clara a ideia de que ninguém necessariamente precisa de profetas, bíblias, pregadores, ou igrejas prepotentes para se tornar tão moralmente perfeito quanto é humanamente possível. Um mapa de Royce serve para deixar precisa a ideia de que, em tese, pode haver dentro de um ser humano uma imagem — um mapa — do Absoluto Infinito do qual esse ser humano finito faz parte. “Não quero um Absoluto estéril, que devore o indivíduo”, Royce escreveu certa vez. Se o homem é uma espécie de figura geométrica com trilhões de detalhes, uma figura que reflete, em menor medida, o Absoluto do qual faz parte, então tem condições de olhar para si mesmo, de investigar-se, e assim também investigar o Absoluto além de si; e para nada disso precisa se submeter a um profeta o qual nunca viu, ou a um livro cheio de contradições e de erros factuais. “Quero um Absoluto que permita o florescimento daqueles que buscam a verdade.”
Mais tarde, mapas de Royce foram usados por matemáticos e por filósofos (especializados em matemática ou em metafísica) para deixar precisas cinco ideias importantes: (1) definições recursivas, (2) o infinito de Dedekind, (3) coisas finitas, (4) complexidade infinita, e (5) complexidade finita.
Definições recursivas. Uma definição recursiva tem sempre três regras: a regra inicial, a regra de sucessão, e a regra de limite. Até onde se sabe, é o único jeito de descrever uma estrutura infinita com número finito de símbolos. Em muitas definições matemáticas, referentes a objetos abstratos infinitos, as três regras estão implícitas.
Infinito de Dedekind. Um conjunto S é infinito, ou é infinito de Dedekind, se e somente se (se-se) existe um subconjunto próprio T de S tal que a cardinalidade de T é igual à de S, isto é, tal que os elementos de T podem ser postos em correspondência um a um (bijeção) com os elementos de S.
Finito. Um conjunto S é finito se-se não é infinito, isto é, se-se S não contém um subconjunto próprio T tal que T tem a mesma cardinalidade de S.
Complexidade infinita. Uma estrutura S é infinitamente complexa se-se S contém uma parte própria T tal que T tem a mesma forma que S. A parte própria T se chama “subestrutura própria de S”; e a parte própria T tem a mesma forma de S se-se existe um isomorfismo de S para T. Se duas estruturas têm a mesma forma, então elas são igualmente complexas; se x tem exatamente a mesma forma que y, então x é tão complexa quanto y. Assim, os mapas de Royce são estruturas infinitamente complexas; e se o Absoluto tem uma estrutura infinitamente complexa, passa a ser razoável a ideia de que cada ser humano contém em si mesmo informação suficiente sobre o Absoluto para, se quiser, levar uma vida tão divina quanto humanamente possível.
Complexidade finita. Um todo é finitamente complexo se-se não é infinitamente complexo. Mais precisamente, um todo S é finitamente complexo se-se, para toda parte própria T de S, T é menos complexa que S.
O mapa de Royce que acabou de ver é útil para pensar sobre as inter-relações entre duas posições importantes na filosofia da matemática atual: ficcionalismo e platonismo. O ficcionalista diz que afirmações como “o número 3 é primo” são uma espécie de ficção; são afirmações aparentadas com “Sherlock Holmes toca violino bastante bem”. A afirmação “Sherlock Holmes toca violino bastante bem” é sobre um personagem de ficção, Sherlock Holmes, que, de acordo com a ficção, é um ótimo detetive e um ótimo violinista; a afirmação “o número 3 é primo” é sobre um personagem de ficção, o número 3, que, de acordo com a ficção, entre outras coisas é primo e divide os inteiros 6, 9, e 12. O platonista, por sua vez, diz que afirmações como “o número 3 é primo” não são uma espécie de ficção; ao contrário, são verdadeiras porque de fato existe um objeto abstrato que é isomórfico com o que o brasileiro chama de “o número três” e o inglês chama de “the number three”. Uma das características desse objeto abstrato é esta: ele só pode ser dividido em três partes iguais de 1 unidade cada uma, ou então em uma única parte de 3 unidades — não há nenhuma outra maneira de dividi-lo em partes iguais de unidades, isto é, o número 3 é primo.
O ficcionalista diz que a matemática é útil porque seus personagens ficcionais são feitos especialmente para que sejam úteis como analogia para os fenômenos do universo. São personagens simples, como pontos, retas, triângulos, números, conjuntos, relações, funções; e o matemático descobre como tais personagens interagem uns com os outros por meio de uma linguagem muito bem comportada, cujo nome é “lógica”. Visto que os personagens matemáticos são simples e que seu comportamento pode ser bem conhecido, eles servem como analogia para os fenômenos que constituem o universo: para investigar algo que não conhece, o homem precisa partir de algo que conhece — de algo que ele mesmo criou; por exemplo, a matemática. O platonista diz que a matemática é útil porque tudo o que existe ou é um objeto abstrato, pura e simplesmente, ou supervém num objeto abstrato. O universo em que vivemos, de acordo com o platonista, é um objeto concreto infinito que supervém numa coleção muito complicada, e também infinita, de objetos abstratos. Ele é, para simplificar um pouco, estritamente idêntico a uma coleção complicada de objetos abstratos. O platonista contemporâneo é um monista: só existem objetos abstratos — nada mais existe além disso. Alguns desses objetos abstratos servem de substrato para universos concretos, ou então, o que é um jeito diferente de dizer a mesma coisa, todo universo concreto supervém num universo abstrato.
Suponha, por um momento, que o platonismo é verdadeiro. Suponha também que a Natureza é infinitamente complexa. Ela inclui o universo em que vivemos (codinome UH), mas também inclui qualquer outro universo que possa existir — assim, o universo UH é subconjunto da Natureza. (Se houver outros universos, daí UH é subconjunto próprio da Natureza.) Por fim, use o mapa de Royce Mω para representar a Natureza.
Se isso for verdade, daí a matemática atual é algo mais ou menos assim:
Tudo o que os matemáticos inventaram e descobriram até hoje está contido dentro dos três círculos vermelhos; é pouco para compreender tudo aquilo que constitui a Natureza. É por isso que, em muitas situações práticas, parece que a matemática é inadequada; parece que é insuficiente. Além disso, é bem possível que grandes trechos da matemática atual não se refiram ao universo UH, mas a partes da Natureza que não fazem parte, de maneira nenhuma, de UH. Talvez se refiram ao que existe em outros universos. Se esse último ponto for verdadeiro, daí tais grandes trechos de matemática são, do ponto de vista de gente excessivamente pragmática, inúteis.
Em outras palavras, usando o mapa de Royce Mω como analogia, é fácil ver que a seguinte hipótese talvez seja verdadeira: a matemática atual é incompleta, em primeiro lugar; e, em segundo lugar, uma parte dela talvez seja completamente inútil para aqueles de inabalável espírito prático, pois não serve para modelar nada que existe concretamente em nosso universo UH. E tudo isso junto explica por que a tese do ficcionalista faz sentido — mesmo que o platonismo seja verdadeiro.
Jorge Luis Borges, o famoso escritor argentino, conhecia alguns dos textos de Josiah Royce, a quem admirava; escreveu várias estórias usando o mapa de Royce como referência. Em 1964, num de seus ensaios, escreveu o seguinte:
As invenções da filosofia não são menos fantásticas que aquelas da arte: Josiah Royce, no primeiro volume de seu trabalho O Mundo e o Indivíduo (1898), formulou o seguinte: “Vamos imaginar que uma porção do solo da Inglaterra foi nivelado à perfeição e que, sobre ele, um cartógrafo traça um mapa da Inglaterra. O trabalho é perfeito: não há detalhe sobre o solo da Inglaterra, por menor que seja, que não esteja registrado no mapa; tudo tem no mapa sua correspondência. Esse mapa, se for assim, deve conter um mapa do mapa, que deve conter um mapa do mapa do mapa, e assim por diante ao infinito.” Por que ficamos inquietos com o mapa dentro do mapa e com as mil e uma noites dentro do livro As Mil e Uma Noites? Por que nos inquieta que Dom Quixote seja um leitor de Quixote e que Hamlet seja um espectador de Hamlet? Acredito que descobri a razão: tais inversões sugerem que, se os personagens de obras ficcionais podem ser leitores ou espectadores, então nós, seus leitores e espectadores, podemos ser ficções.
Talvez a realidade platônica seja uma ficção criada pelo homem. Talvez o homem seja apenas um personagem, entre infinitos outros, cuja existência é dádiva de entidades platônicas. Talvez o platonismo seja verdadeiro, afinal de contas, mas o homem só pode explorar a realidade platônica por meio de suas ficções, especialmente as ficções de caráter matemático. {FIM}
Observações:
1. Não estou dizendo que nosso universo UH é infinitamente complexo, isto é, que uma parte própria dele é isomórfica com UH inteiro.
2. Mesmo que o universo UH não seja infinitamente complexo, um mapa de Royce serve para mostrar que uma parte de UH pode conter muita informação sobre todo o resto de UH. Assim, não é absurdo pensar que a cultura humana, tomada como um todo (incluindo a ciência), é uma parte de UH na qual há bastante informação sobre UH como um todo.
3. O mapa de Royce Mω tem duas propriedades: (a) Se os lados de M0 medem x unidades de comprimento, a área do mapa mede x2 unidades de área; (b) O perímetro total do mapa, incluindo as linhas internas, mede 8x unidades de comprimento. Provar a propriedade (b) é um bom exercício para quem está começando a lidar com séries infinitas. Depois, vale a pena comparar o mapa de Royce Mω com a curva de Koch para escrever um ensaio: Por que o comprimento do perímetro de Mω é finito, mas o da curva de Koch é infinito?
4. Para saber mais sobre isomorfismos, veja a postagem Filosofia da Mente: O Mapa e o Território.
5. Para saber mais sobre o conceito de superveniência, veja a observação 5 no pé da postagem O “Zaratustra” de Nietzsche e a Liberdade do Matemático.
6. Quando uso o termo “homem”, em geral quero dizer o conjunto dos elementos x tais que x é um indivíduo da espécie humana.
7. Você viu no texto: talvez a existência de todas as coisas, incluindo o homem, seja um presente de entidades platônicas. Lembrete: segundo o platonismo contemporâneo, entidades platônicas não têm mentalidade. Elas não são entidades conscientes; elas não são pessoas. Ao contrário, são semelhantes ao processo de modificação das espécies por seleção natural, que não tem mentalidade, mas que é capaz de feitos maravilhosos de engenharia.