Cálculo Tornado Fácil 2

Baseado no livro de Silvanus P. Thompson

Lembrete: O texto a seguir é parte de uma sequência; ele começa na seção 5 porque o texto anterior terminou na 4. Os textos da sequência até agora são Cálculo Tornado Fácil 1, CTF 2, CTF 3, CTF 4, CTF 5, CTF 6, CTF 7, e CTF 8.

---

---

{5}/ Capítulo 3

Sobre crescimentos relativos

Por todo o cálculo você lida com quantidades que crescem, e com taxas de crescimento. Pode classificar todas as quantidades em duas classes: constantes e variáveis. Aquelas que julgar de valor fixo, que chamará de constantes, pode denotar algebricamente com as primeiras letras do alfabeto, tais como a, b, ou c; aquelas que julgar capazes de crescer, ou de variar (como os matemáticos dizem), pode denotar com as últimas letras do alfabeto, tais como x, y, z, u, v, w e, às vezes, t.

Além do mais, em geral você se ocupa com mais de uma variável ao mesmo tempo, e pensa no modo como uma depende de outra: por exemplo, pensa no modo como um projétil atinge determinada altura e, para tanto, precisa de tempo para chegar à tal altura. Ou considera um retângulo de determinada área fixa, e se pergunta como um acréscimo no comprimento dele significa um correspondente decréscimo na largura. Ou pensa no modo pelo qual, ao variar a inclinação de uma escada contra a parede, faz variar a altura que ela alcança.

Então supõe que tem duas dessas variáveis que dependem uma da outra. Justamente por causa dessa dependência, uma alteração numa delas produz uma alteração na outra. E daí chama uma dessas variáveis de x, e a outra, que depende dela, de y.

Você obriga x a variar; quero dizer: ou altera seu valor ou imagina seu valor alterado, e faz isso ao adicionar um pouquinho a x — o tal pouquinho cujo nome é dx. Sendo assim, obriga x a se transformar em x + dx. Daí, visto que alterou x, alterou y também (por causa da relação de dependência), e transformou y em y + dy. Aqui, o pouquinho dy às vezes é positivo, às vezes, negativo, e não será do mesmo tamanho que dx, exceto, é claro, por um milagre.

Que tal pensar em dois exemplos?

Figura 4

(1) Imagine x como sendo a base de um triângulo retângulo, e y como sendo a altura (tal como vê na figura 4 logo acima), de modo que o ângulo entre a base e a hipotenusa esteja fixado em 30 graus. Se supõe que o triângulo vai se expandir, mas mesmo assim manterá os ângulos internos tais como na situação original, então, conforme a base cresce para se transformar em x + dx, a altura se transforma em y + dy. Neste caso, o crescimento de x provoca o crescimento de y. O triângulo pequeno, cuja base é dx e cuja altura é dy, é semelhante ao triângulo original; daí percebe com clareza que o valor da razão dy/dx é igual ao valor da razão y/x. Como o ângulo é de 30 graus, verá em breve que:

Lembrete. Aqui, Silvanus reconheceu que y/x é a mesma coisa que sen(30°)/cos(30°), isto é, tan(30°), cujo valor exato é 1/√3.

(2) Olhando a figura 5, imagine x como sendo a distância horizontal da parede ao pé da escada AB, cujo tamanho é fixo; e imagine y como sendo a altura do topo da escada na parede (como sendo OB). Vê que y depende de x? Então, vê também que, se puxa o pé da escada A para um pouco mais longe da parede, o topo da escada B desce um pouquinho. Reafirme isso com a linguagem do cálculo: se aumenta x para x + dx, daí y se transforma em y – dy; em outras palavras, quando adiciona um incremento positivo a x, também adiciona um incremento negativo a y.

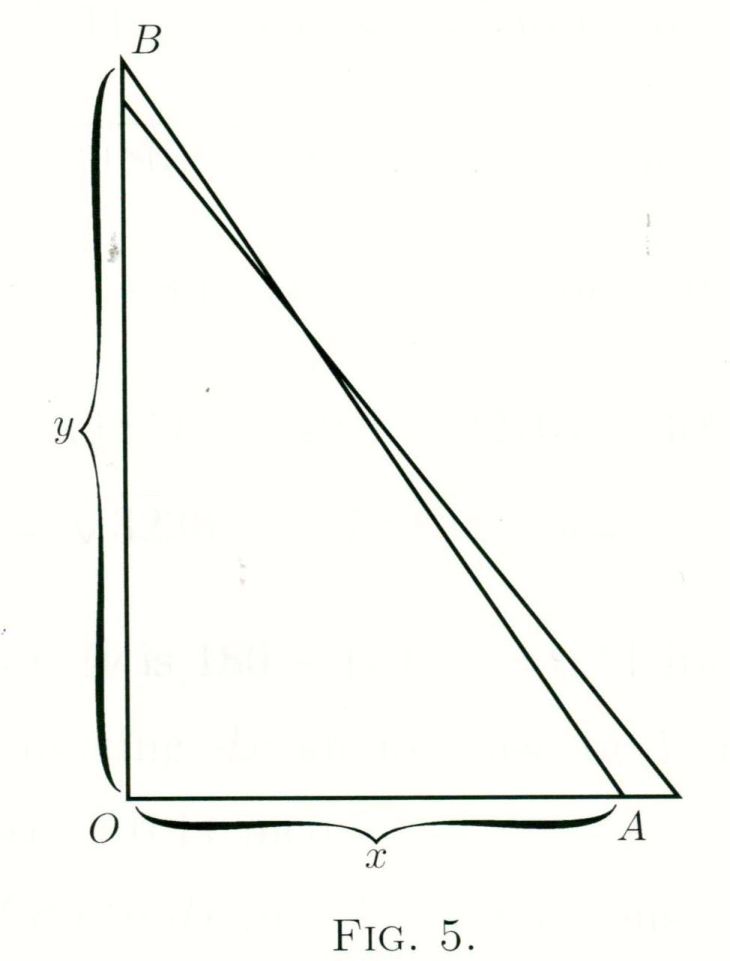
Tudo bem, mas quais são os valores? Você supõe que a escada é comprida o suficiente para que, quando o pé A está a 21 centímetros da parede, o topo B está a 2 metros e 20 centímetros de altura. Agora, se você puxa o pé da escada 1 centímetro para mais longe da parede, quantos centímetros o topo baixará? Ao pôr tudo em centímetros, vê que começa com x = 21 cm e y = 220 cm. Então o valor que adicionou a x, e que deve chamar de dx, é 1 centímetro; isto é, x + dx = 22 cm.

Até que ponto y ficará menor? Ora, a nova altura tem de ser y – dy. Se usa o teorema de Pitágoras para achar o comprimento da escada, chega a 221 centímetros [que é √(21² + 220²)]; e a partir desse passo está pronto para achar o valor de dy. Então, a nova altura, que é y − dy, tem de ser tal que:

O que é isso? “O quadrado da hipotenusa é igual à soma dos quadrados dos catetos”; é o que tem recitado na escola há anos. Como y = 220, daí dy tem de ser quase 1 milímetro. As contas são:

Portanto, viu que ao tornar dx equivalente a um acréscimo de 1 centímetro, obteve dy equivalente a um decréscimo de 1 milímetro. Com tais informações, já pode expressar a razão entre dy e dx:

Com um pouco de imaginação, pode ver que, com exceção de uma posição em particular, dy é sempre de tamanho diferente de dx.

Bem, ao longo dos estudos de cálculo diferencial, você caçará, caçará e caçará uma coisa curiosa, uma mera razão, qual seja, a proporção que dy mantém em relação a dx enquanto os dois ficam tão pequenos quanto queira.

Devo avisá-lo sobre o fato de que só pode achar essa razão dy/dx quando y e x estão correlacionados de alguma forma, de modo que sempre que x varia, y varia também. No primeiro exemplo que examinou, conforme a base x do triângulo aumenta, sua altura y aumenta também; no segundo, conforme a distância x da base da escada à parede aumenta, a altura y da escada sobre a parede diminui de um jeito análogo, primeiro devagar, e depois mais e mais depressa conforme x se torna cada vez maior. Nos dois casos, você definiu perfeitamente a relação entre x e y, e agora pode expressá-la matematicamente. No primeiro caso, basta reconhecer que y/x = tan(30°); no segundo, que x² + y² = c² (sendo c o comprimento da escada); em ambos, dy/dx tem o significado que achou.

Agora, mantenha x como antes, isto é, como a distância do pé da escada à parede, porém faça y representar outra coisa, como a quantidade de tijolos que usou para construir a parede ou o número de anos desde que a pintou pela última vez. Nestes dois casos, qualquer mudança que faça no valor de x não produzirá nenhuma mudança no valor de y, e não poderá atribuir nenhum significado sensato à razão dy/dx. Aliás, achará impossível achar uma expressão sensata para representá-la. [Quanto à palavra “sensata”, veja o texto da seção 7.] Quero dizer: sempre que usar os diferenciais dx, dy, dz, etc., estará assumindo algum tipo de relação entre x, y, z, etc., e essa relação é (com frequência) chamada de “função” de x, y, z, etc. Caso examine de novo as duas expressões dos dois exemplos [y/x = tan(30°) e x² + y² = c²], terá então examinado duas funções de x e y. Tais expressões contêm, implicitamente, os meios pelos quais pode denotar tanto x em função de y quanto y em função de x. (Uso o advérbio “implicitamente” porque elas contêm o modo pelo qual denotar uma variável em função da outra, mas não mostram claramente qual é.) Por tal motivo, pode dizer que se referem a y como função implícita de x, ou que se referem a x como função implícita de y, conforme escolhe qual variável depende de qual. Com pouco trabalho, contudo, consegue colocá-las nas formas a seguir:

Com as expressões acima, você afirma explicitamente (isto é, distintamente) o valor de y em termos de x ou o valor de x em termos de y, e por esse motivo pode chamá-las de funções explícitas de x ou de y. Por exemplo, x² + 3 = 2y − 7 é uma função implícita de x e y; mas pode reescrevê-la como y = (x² + 10)/2 (em que y é função explícita de x) ou como x = √(2y – 10) (em que x é função explícita de y). Vê então que, mais simplesmente, uma função explícita de x, y, z (etc.) é uma variável cujo valor muda quando x, y, z (etc.) também mudam, seja uma de cada vez ou várias de uma vez. Por causa disso, pode chamar o valor da função explícita de variável dependente, pois depende do valor das outras quantidades na função; e pode chamar essas outras variáveis de variáveis independentes, pois seu valor independe do valor assumido pela função. Por exemplo, se u = x²senθ, x e θ são as variáveis independentes, e u é a variável dependente. [Sobre esse assunto, veja também o texto da seção 8.]

Às vezes, você não sabe qual é a relação exata entre as quantidades x, y, z, ou até sabe, mas não quer colocá-la no papel; apenas sabe, ou apenas quer afirmar, que existe algum tipo de relação entre as quantidades. Para indicar a existência de uma função de x, y, z, pode usar a notação F(x, y, z) = 0 caso queira denotar uma função implícita, ou pode usar a notação x = F(y, z), y = F(x, z) ou z = F(x, y) caso queira denotar uma função explícita. Às vezes, no lugar de F, um autor usa a letra f ou a letra φ ou a letra g, de modo que, ao escrever y = F(x), y = f(x), y = φ(x) ou y = g(x), ele quer dizer a mesma coisa, isto é, que o valor de y depende do valor de x de alguma maneira não especificada, maneira essa batizada de F, f, φ, ou g.

Matemáticos se referem à razão dy/dx com palavras do tipo “coeficiente diferencial de y em relação a x” ou do tipo “função derivada de y em relação a x” ou do tipo “derivada de y no ponto x”. São nomes científicos solenes para algo singelo. Mas você não deve se deixar intimidar por nomes solenes, quando a matéria em si é tão fácil. No lugar de se intimidar, pode pronunciar uma breve maldição contra a estupidez de nomes trava-língua e, tendo assim aliviado a mente, ir adiante e tratar a matéria em si, isto é, a razão dy/dx.

Na álgebra comum que estudou no ensino básico, você estava sempre caçando alguma quantidade desconhecida, que em geral chamava de x ou de y; ou às vezes tinha de caçar duas quantidades desconhecidas de uma vez. Agora, deve aprender a caçar de um jeito novo, pois a raposa não é mais nem x nem y; em vez dela, é esse curioso filhote chamado dy/dx. Bem, o processo de achar uma fórmula com a qual consiga calcular o valor de dy/dx é chamado de “derivação”. Contudo, lembre-se: o que está caçando é o valor dessa razão nos casos em que tanto dy quanto dx são infinitamente pequenos. Dizendo isso de outra forma, o verdadeiro valor do coeficiente diferencial é aquele valor para o qual o coeficiente se aproxima quando você vai atribuindo para dx (e, por tabela, para dy) valores cada vez menores; ou, para usar uma expressão frequente, quando vai atribuindo para dx valores tão pequenos quanto queira, até que estejam infinitamente miúdos.

Vamos agora estudar como sair à procura de dy/dx.

---

---

{6}/ Nota ao capítulo 3

Como ler derivadas

Espero que jamais caia no erro de vários alunos, o de achar que dx significa d vezes x, pois d não é um fator — ele significa “um infinitésimo de” ou “um pedacinho de” ou “uma fraçãozinha de” seja lá o que estiver na frente de d. Leia dx assim: “dê-xis”.

Caso o leitor não tenha a quem consultar para tirar dúvidas de pronúncia, basta saber que deve ler coeficientes diferenciais da seguinte maneira:

Ao ver o coeficiente (A), deve pronunciar “dê-ípsilon por dê-xis” ou “dê-ípsilon sobre dê-xis”. Quanto ao coeficiente (B), deve pronunciar “dê-ú por dê-tê” ou “dê-ú sobre dê-tê”.

Mais tarde, estudará coeficientes diferenciais de ordem mais alta. [Ou derivadas de ordem mais alta.] Eis a aparência de um deles:

Quanto à pronúncia, diga “dê-dois-ípsilon por dê-xis-ao-quadrado”; significa que realizou a operação de derivar y em relação a x duas vezes. [Achou a derivada de y em relação a x e, depois disso, achou a derivada da derivada de y em relação a x.]

Outro jeito de indicar que uma função foi derivada é colocar um acento no símbolo da função. Se escreve y = F(x), quer dizer que y varia em função de x de alguma forma não especificada, forma essa batizada de F, e pode escrever F’(x) no lugar de d(F(x))/dx. De modo análogo, ao escrever F’’(x), diz ao leitor que derivou a função F(x) duas vezes em relação a x.

---

---

{7}/ Por que Silvanus usou a palavra “sensata”

Existem funções nas quais uma variação em x não provoca nenhuma variação em y. Por exemplo:

Com essa linha, você diz que y é função de x, e que y vale 3 para qualquer valor de x. Sendo assim, quando deixa x crescer para se transformar em x + dx, y cresce para se transformar em y + dy, cujo valor continua sendo, contudo, 3. Portanto, dy = 0 e, ao fazer as contas, vê que dy/dx = 0.

Note que fez uma mudança em x, mas não provocou nenhuma mudança em y; e no entanto é perfeitamente sensato dizer que dy/dx = 0. Por que Silvanus usou a ideia de “insensato”? Por convenção, se você diz que y é função de x, mas apresenta uma fórmula na qual x não aparece, daí dy/dx = 0. Por exemplo:

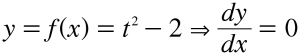
Com essa linha, quis dizer: “Afirmo que y é função de x. Contudo, apresento uma fórmula em que x não aparece; no lugar dele, aparece a variável t. Sendo assim, uma variação em x não provocará nenhuma variação em y, já que na verdade y depende de t, e não de x, e por isso, por convenção, dy/dx = 0.”

Ao usar a ideia de “insensatez”, Silvanus provavelmente pensava nesse segundo cenário.

---

---

{8}/ Funções explícitas e implícitas

Aqui, Silvanus fez uma simplificação com a qual você precisa tomar cuidado. Suponha, por exemplo, um professor malvado, em cuja prova pede aos alunos que digam qual é a derivada da função a seguir:

(O símbolo triangular é o operador lógico “&”. Neste caso, significa que as duas expressões devem ser verdadeiras ao mesmo tempo.)

Como o professor expressou x em função de y, o estudante distraído talvez chegue à seguinte derivada:

Mas não era isso o que o professor queria saber. Embora ele tenha expressado x em função de y, ele também disse, com y = f(x), que y é a variável dependente e que x é a variável independente, e portanto o que queria saber é a derivada a seguir:

Enfim: em muitos casos, o estudante pode começar com uma fórmula para y em função de x, e depois rearranjá-la para representar x em função de y, mas muitas vezes, apesar do rearranjo, ainda está tratando de y em função de x. Em casos assim, para eliminar qualquer possibilidade de ambiguidade, faz bem ao usar o símbolo f(x) no lugar de y:

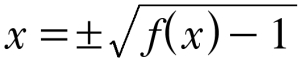
Aqui, embora x esteja isolado do lado esquerdo da igualdade, fica claro que é a variável independente e que, por conveniência, foi expressa em função da variável dependente.

---

---

{9}/ Capítulo 4

Os casos mais simples

Agora verá como, a partir dos primeiros princípios, pode derivar algumas expressões algébricas simples.

Caso 1. Comece com a expressão y = x². O primeiro passo é lembrar que, no cálculo, a ideia fundamental é a de crescimento. (Os matemáticos preferem dizer variação.) Como y e x² são iguais um ao outro, pode apostar que, quando x cresce, x² cresce também. Mas o que deve descobrir é a proporção entre o crescimento de y e o de x. Em outras palavras, deve descobrir a razão entre dy e dx, ou, mais brevemente, o valor de dy/dx.

Então, você permite que x cresça um pouquinho de nada, e se transforme em x + dx; de modo similar, y crescerá para se transformar em y + dy. Olhando a expressão y = x², pode ver com clareza que o y aumentado tem de ser igual ao quadrado do x aumentado. Sendo assim, agora pode usar a notação matemática e escrever:

Ao expandir o lado direito da equação, obterá:

O que (dx)² significa? Você lembra que dx significa “um infinitésimo de” — uma fraçãozinha minúscula de x. Então (dx)² significa uma fraçãozinha de uma fraçãozinha de x; e já sabe, pois já leu o capítulo 2, que isso é uma quantidade pequena na segunda ordem de magnitude, ou na segunda ordem de pequenez. Portanto, ao comparar (dx)² com os outros termos da expressão, pode desconsiderá-lo, especialmente se faz dx muito, muito pequeno. Deixando (dx)² de fora, fica com:

Sabe que y = x²; sendo assim, ao subtrair y do lado esquerdo da igualdade e x² do lado direito, fica com:

Pode dividir os dois lados por dx, e agora obtém:

Veja: era exatamente isso que você queria descobrir. Neste caso, a razão pela qual y cresce em relação ao crescimento de x, conforme x cresce um pouquinho de nada, é 2x.

Exemplo numérico — Você supõe que x = 100 e que, por consequência, y = 10.000. Deixa x crescer até que vire 101 (ou seja, dx = 1).  Daí o y aumentado será igual a 101 × 101 = 10.201. Contudo, se concordou que pode ignorar pequenas quantidades de segunda ordem de magnitude, pode rejeitar 1 em comparação com 10.000, e arredondar o y aumentado para 10.200.  Vê que y cresceu de 10.000 para 10.200; dy, o pedacinho adicionado a y, vale 200.

De acordo com a álgebra da passagem anterior, verifica que dy/dx = 2x. É o que deve ser mesmo: x = 100 e 2x = 200.

“Eu protesto!”, você talvez sinta vontade de me dizer. “Eu protesto porque desprezamos uma unidade inteira!”

Ora, então tente de novo, desta vez igualando dx a uma porçãozinha ainda menor. Por exemplo: você fixa dx em 1/10, e daí x + dx vira 100,1; como resultado:

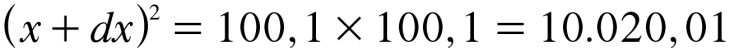
Nota que o último algarismo 1 é apenas um milionésimo de 10.000, e é completamente desprezível; pode considerar 10.020 sem o pequeno decimal. Com isso, fixa dy em 20, e daí:

Vê que a razão entre os dois infinitésimos (ou o coeficiente diferencial) continua valendo 2x. [Sobre isso, veja o texto da seção 11.]

Caso 2. Tente derivar y = x³ com o mesmo método: faz x crescer até que vire x + dx, e daí y cresce até que vira y + dy. Com isso, obtém:

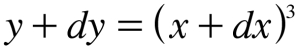
Ao expandir o lado direito da igualdade, chega a:

Já sabe que pode omitir as quantidades de segunda e de terceira ordem de magnitude (ou de pequenez), visto que, quando dy e dx são ambos feitos tão pequenos quanto queira, (dx)² e (dx)³ ficam muito, muito menores em comparação. Sendo assim, ao tachar os dois de “desprezíveis”, chega a:

Sabe que y = x³, e que pode retirar y do lado esquerdo da igualdade e x³ do lado direito, para obter:

Caso 3. Agora, você tentará derivar y = x⁴. Começa como antes: deixa x crescer para virar x + dx e faz as contas para ver como y cresce até virar y + dy.

Lembra que pode tirar y do lado esquerdo da igualdade e tirar x⁴ do lado direito, pois y = x⁴, e que pode omitir todos os termos que contenham ordens mais altas de dx, pois, em comparação com os outros termos, são desprezíveis quando dx é bem pequeno. Daí fica com:

* * *

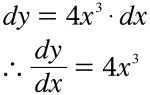
Todos esses casos são fáceis. Ao recolher os resultados que obteve até agora, é bem possível que enxergue um padrão. Você os põe em duas colunas, com os valores de y à esquerda e os valores de dy/dx à direita, e rascunha a tabela a seguir.

Apenas olhe para os resultados: parece que a derivação tem o poder de reduzir o expoente de x por 1 unidade (no caso da última linha da tabela, de reduzir x⁴ para x³) e de, ao mesmo tempo, multiplicar a potência por um coeficiente (que é o mesmo número que antes funcionava como expoente). Você vê isso e em seguida parte para uma conjectura: todas as outras potências inteiras e positivas de x vão funcionar da mesma maneira. Assim, você espera que, ao derivar x⁵, obterá 5x⁴; ao derivar x⁶, obterá 6x⁵. Caso vacile, tente derivar uma dessas funções para ver se a hipótese se confirma. Tente, por exemplo, derivar y = x⁵.

De novo, despreza todos os termos que contêm pequenas quantidades de ordem maior de pequenez, e fica com:

Já sabe que pode subtrair y de um lado e x⁵ do outro, pois são iguais; com isso chega a:

E isso confirma sua hipótese.

* * *

Ao seguir os passos lógicos da hipótese, conclui que, se deseja lidar com qualquer expoente maior (por exemplo, um expoente n), deve aplicar a mesma regra, isto é:

Sendo assim, se n = 8, daí y = x⁸ e, ao realizar os passos da derivação, obtém dy/dx = 8x⁷.

E, de fato, como qualquer tabela de derivadas mostra, a regra pela qual partir da função xⁿ e chegar à derivada nxⁿ⁻¹ é verdadeira para todos os casos nos quais n é inteiro e positivo. (Pode provar essa afirmação caso recorra ao teorema do binômio de Newton.) Mas precisará investigar um pouco mais para ver que também pode aplicar a mesma regra quando n assume valores negativos ou fracionários.

O caso do expoente negativo. Você começa com y = x^–2, deixa x crescer para virar x + dx, e com isso deixa y crescer para virar y + dy. Grava esse fato como já fez antes:

Reescreve o lado direito da igualdade:

Usando o teorema binomial para expandir isso, obterá:

Ao desprezar as quantidades de ordens maiores de magnitude (ou de pequeneza), e ao reconhecer que y = x^–2 e que pode ser tirado dos dois lados, chega a:

O que está de acordo com a hipótese geral.

Caso do expoente fracionário. Começa com y = √x = x^1/2. Daí, basta realizar todos os passos como já fez antes:

Ao subtrair y = x^1/2 dos dois lados da função original, e ao desprezar os termos de maior grau de magnitude, fica com:

Em outras palavras, chega a outra versão válida, de acordo com a regra geral que acabou de conjecturar.

Resumo. Você chegou longe, pois já conhece a regra de derivação mais famosa de todas, a regra da potência: para derivar xⁿ, multiplique a base pelo expoente, e reduza o expoente por 1 unidade, obtendo ao fim do algoritmo nxⁿ⁻¹.

---

---

{10}/ Exercícios I

Derive as expressões abaixo.

Você aprendeu a derivar potências de x. Viu como é fácil?

---

---

{11}/ Por que desprezar (dx)²

Outro jeito de ver isso, no caso de y = x², é usar um recurso comum no ensino fundamental: a matriz de multiplicação. Com essa matriz, o aluno do ensino fundamental controla melhor a distribuição da multiplicação sobre a adição.

Funciona assim: monte uma tabela na qual anota, na linha do topo, o primeiro fator ou as parcelas do primeiro fator; e na coluna mais à esquerda, o segundo fator ou as parcelas do segundo fator. Daí use cada uma das células da tabela para realizar a multiplicação, e por último some os termos contidos nas células interiores. Veja como a tabela fica o caso de (x + dx)², isto é, (x + dx) · (x + dx):

O resultado disso é x² + 2x∙dx + (dx)². Se x = 100, a tabela relativa a (100 + dx)² fica assim:

O resultado é 10.000 + 200∙dx + (dx)². Fica claro que, quanto menor o valor de dx, mais desprezível fica o termo (dx)², e que neste caso dy/dx = 2x para qualquer valor de x.

Será?

Bem, muito estudante, e muito professor, detesta essa história de “desprezar os termos de ordem mais alta de magnitude”, pois não querem desprezar nenhum termo até que tenham absoluta certeza. Neste caso, há outro jeito de realizar a conta acima, e que sempre dá certo quando o coeficiente diferencial existe.

Você começa com y = x². Deixa x crescer para virar x + dx, e com isso y vira y + dy:

Agora, como próximo passo, tira y do lado esquerdo da igualdade e x² do lado direito, pois são iguais:

Neste ponto, dá o passo decisivo, diferente do passo explicado por Silvanus: divide todos os termos da expressão por dx, sem desprezar nenhum deles:

Fica em condições de notar que, conforme dx tende a zero (sem jamais se igualar a zero), a razão dy/dx tende a 2x (sem jamais se igualar a 2x); portanto, o limite da razão dy/dx, conforme dx tende a zero, é 2x. Você sempre pode reescrever uma derivada como sendo um limite, e esse jeito de fazer as contas equivale a dizer, talvez ingenuamente, “despreze os termos multiplicados por ordens mais altas de dx”.

---

---

{12}/ Lembrete: o teorema binomial

Para todo inteiro positivo n, o que significa (x + y)ⁿ?

Para usar o teorema na regra da potência, troque y por dx e terá a receita de como expandir (x + dx)ⁿ.

Há uma versão do teorema binomial para expoente negativo, que Silvanus usou no texto, e que não aparece na expressão acima, mas pode obtê-la facilmente: ponha a expressão acima no denominador, e trabalhe com a diferença entre o que você tem e o que gostaria de ter. Por exemplo:

---

---

{13}/ A regra da potência

Se y = f(x) = xⁿ, na verdade dy/dx = f’(x) = nxⁿ⁻¹ para todo n real; em outras palavras, a regra vale não só para expoentes inteiros e fracionários, mas também para expoentes irracionais. Depois que o estudante já conhece a regra da cadeia (que Silvanus ainda não explicou) e o método da derivação implícita de expressões logarítmicas (idem), a prova disso fica muito fácil.

Começa com a relação entre y e x:

Tira então o logaritmo natural de todos os termos da igualdade, o que mantém a igualdade verdadeira (se y > 0, claro):

Usa uma propriedade dos logaritmos: pode reescrever ln(xⁿ) como nlnx.

Agora deriva a expressão toda implicitamente, sabendo duas coisas: que a derivada de lnx é 1/x e que y representa uma função, isto é, ao derivar lny terá de aplicar a regra da cadeia. Feito isso, basta usar a álgebra do ensino médio para ajeitar tudo.

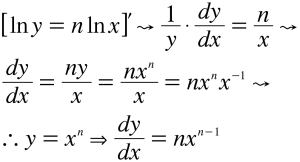
Caso o leitor não tenha compreendido todas as passagens, não se preocupe: elas serão explicadas nos próximos capítulos. Por enquanto, basta se habituar com a última linha, que representa a famosa regra da potência e que vale para qualquer valor real de n.

---

---

{14}/ A derivada em linguagem e notação atuais

Fig. A

Silvanus usa uma nomenclatura comum no século 20, especialmente entre cientistas e engenheiros, mas que tem sido pouco usada por professores de matemática. Em vez de chamar dy/dx de “coeficiente diferencial”, os matemáticos preferem a palavra “derivada”; em vez de chamar dx de “um infinitésimo de x”, eles preferem “o diferencial de x”. Quanto ao que a derivada significa, raciocinam mais ou menos assim:

(1) Considere a função y = f(x).

(2) Suponha que uma pequena mudança δx em x provoca uma mudança δy em y, de modo que:

(3) A derivada da função f, que você pode denotar com dy/dx, df/dx, y’ ou f’(x), entre outros símbolos, é o limite da expressão acima conforme δx tende a zero — caso tal limite exista. (Essa parte é importante: nem sempre o limite existe.)

(4) Os matemáticos já provaram que achar a derivada é completamente equivalente a achar a inclinação da reta tangente à função f no ponto x sob estudo. {FIM}

---

Observações:

1. Não se esqueça de que Silvanus se esforçou para não mencionar detalhes técnicos importantes em seu curso de introdução ao cálculo. (Coisa que eu, o redator deste blogue, nem sempre respeitei, como pode ver ao examinar as seções 13 e 14.) Caso o leitor queira estudar uma introdução com todos os detalhes técnicos no lugar, clique aqui.

2. Para ler a próxima parte desta série, clique aqui.