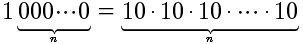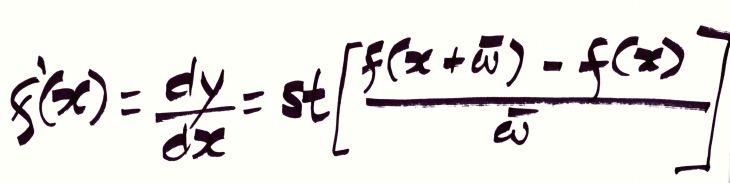
{0}/ Introdução
Este é o sexto capítulo sobre como você usa o sistema dos números hiper-reais para construir o cálculo diferencial e integral. (Eis os cliques para os outros capítulos: primeiro, segundo, terceiro, quarto, quinto, sétimo, oitavo, nono, décimo.) Desta vez, o assunto é cálculo diferencial, que significa, para resumir bastante: “Medir, instante a instante, a velocidade com que as coisas mudam.” Lembretes: a seção a seguir é a 56 porque o capítulo anterior terminou com a seção 55; e “figura §56-1” significa “a primeira figura que vai encontrar na seção 56”.
Com esses seis primeiros capítulos, você já tem condições de usar derivadas e integrais na resolução de uma quantidade muito grande de problemas práticos e teóricos.

{56}/ Variações na distância Terra-Lua
Suponha que certa magnitude y esteja crescendo ou diminuindo em função de certa magnitude x; se quiser, escreva «posso ver y como sendo função de x» desta maneira: y = f(x). Dois exemplos: a temperatura y de um forno varia conforme a passagem do tempo x; a distância y da Terra à Lua varia conforme a passagem do tempo x. E daí é natural que pergunte: [1] quando x = 5 segundos, e a temperatura do forno era de y = 31 graus, a que velocidade a temperatura y subia ou descia? Ou ainda que pergunte: [2] quando x = 17 horas e 17 minutos do dia 23 de fevereiro de 2016, e a distância da Terra à Lua era de y = 400.820 quilômetros (veja o gráfico §56-1), a que velocidade a distância y da Terra à Lua aumentava ou diminuía?
Bem, no dia 23 de fevereiro, quando x = 17:17, y = 400.820 quilômetros; mas, quando x = 17:22, y = 400.828 quilômetros. Se divide a variação Δy da distância pela variação Δx do tempo, obtém a variação média naqueles 5 minutos:


Figura §56-1: O gráfico da variação da distância entre a Terra e a Lua.
No dia 23 de fevereiro de 2016, às 17:17, a distância entre a Terra e a Lua aumentava mais ou menos à taxa de 26,7 metros por segundo — ou, fazendo as contas de outro modo, aumentava à taxa de ≊96 quilômetros por hora.
Ao estudar cálculo diferencial, você estuda métodos e técnicas pelos quais responde a perguntas do tipo [1] e [2], mas com uma diferença: com o cálculo diferencial, você descobre não a variação média de certa quantidade y no intervalo entre x = x0 e x = x1, mas a variação instantânea em certo valor de x; por exemplo, x = x0. A questão é que você não quer fazer a conta com uma diferença entre x0 e x1 de 5 minutos, nem de 1 minuto, nem de 1 segundo, nem de 1 milésimo de segundo. Você quer fazer a conta com uma diferença menor do que qualquer diferença real que possa imaginar — em outras palavras, com uma diferença infinitesimal.
Um professor de matemática, ao apresentar tais ideias pela primeira vez ao aluno, talvez diga algo mais ou menos na linha:
“A derivada de uma função f em cento ponto x = x0 é um número real, com o qual você mede a taxa de mudança de f(x) conforme x passa por x0.”
Alguns alunos entendem essa ideia mais depressa, e outros, mais devagar; mas todos precisam de uns poucos anos para compreendê-la com perfeição. Como disse o professor Nílson José Machado na matéria Cálculo no Ensino Médio: já Passou da Hora: “Quanto à ideia de derivada, nasce assim: quando uma coisa varia com o tempo, é muito natural que eu queira saber como ela varia. Em outras palavras, é muito natural que eu procure uma regularidade nessa variação. Caso eu ache uma regularidade, daí posso dizer coisas do tipo ‘ontem esta árvore estava crescendo à taxa de cinco centímetros por mês’, ‘quando começamos a entrevista, a temperatura desta sala estava subindo à taxa de dois graus centígrados por hora’.” Bem, isso é completamente equivalente à ideia de achar o gradiente (ou a inclinação) da reta tangente à curva de y = f(x) no ponto em que x = x0.
O segredo do cálculo diferencial é olhar um ponto da linha curvilínea de f e, com a imaginação, ver uma reta tangente àquele ponto, e daí, naquele ponto, tratar a função f como se fosse aquela reta tangente. Mexer com linhas retas é muito mais fácil que mexer com linhas curvilíneas — pergunte a qualquer um. Até matemáticos pensam assim, ou, melhor dizendo, principalmente matemáticos.

{57}/ Curvas e suas tangentes
Como calcula o gradiente da função contínua f se f é uma linha reta, do tipo y = f(x) = mx + k, sendo que m, k são dois números quaisquer?
Já viu isso no ensino médio, pois a equação da reta é uma das primeiras lições de geometria analítica. Veja de novo o que acontece quando calcula o gradiente Δy/Δx:


Figura §57-1
Diga que o formulário acima é válido sempre que x1 – x0 ≠ 0; nem precisa tomar o cuidado de escolher x0 < x1, pois, desde que faça x0 ≠ x1, chegará ao valor correto de m qualquer que seja o valor que atribua a x0, x1. Em outras palavras, acha o valor correto de m qualquer que seja o valor não nulo de Δx.
Percebe que está a um passo de generalizar essa ideia para qualquer infinitésimo ϖ ≠ 0?
* * *
Antes de perseguir esse pensamento na sua imaginação, explore uma questão de linguagem: o que o gradiente de f tem a ver com a palavra “tangente”? Olhando para a figura §57-2: é que o gradiente m de f e a tangente de θ são dois números reais completamente equivalentes.
A figura §57-2 é só uma reforma da figura §57-1: ponha um círculo unitário com centro em (c, 0), marque os comprimentos relativos a cosθ, senθ, e use o que sabe sobre semelhança de triângulos. Eis o que deve obter:


Figura §57-2
Com essa expressão, você demonstra uma ideia importante: sempre que cosθ ≠ 0, tanto faz se apresenta a equação de f como y = f(x) = mx + k ou como y = f(x) = (tanθ)x + k. O gradiente da curva de f é constante e vale m = tanθ; e se quer saber qual é o ângulo entre a curva de f e o eixo X, ache o ângulo θ tal que θ = tan–1(tanθ) = tan–1(m).
Um pouco de teoria sobre o ângulo θ. Note que não pode definir tanθ quando θ = π/2, pois cos(π/2) = 0. Apesar disso, pode perfeitamente imaginar e desenhar a reta vertical x = b, cujo ângulo θ com o eixo X mede π/2. Além disso, muitos professores misturam, sem perceber, os dois significados da palavra “gradiente”: um deles é Δy/Δx = tanθ; o outro é a própria medida do ângulo θ. Numa conversa ou palestra, talvez o professor diga: “O gradiente dessa reta é 1.” Quis dizer tanθ = 1. Dez minutos depois: “Bem, visto que o gradiente desta reta é 45 graus, podemos concluir isso e aquilo.” Quis dizer θ = π/4.
Sobre θ = π/2. Quando Δx = 0 ou θ = π/2, você está falando da linha reta vertical x = b, que pode ver como uma relação entre y e x (para todo valor de y, x = b; veja a figura §57-3), mas não pode ver como uma função y = f(x). Para ter uma função, para cada valor de x, deve atribuir um e só um valor de y.

Figura §57-3
* * *
Quando a curva de uma função contínua f não é mais uma reta, mas sim curvilínea, em geral você obtém um valor distinto para tanθ para cada valor distinto que atribui a Δx; ou seja, se escolhe quatro valores distintos para x1, é bem possível que calcule quatro valores distintos para tanθ. É o que pode ver na figura §57-4.

Figura §57-4
Desenhe qualquer curva f contínua, contudo, e vá atribuindo valores para x1 cada vez mais próximos de x0, ou seja, a cada rodada deixe menor o valor de Δx. Daí vê que, quando é capaz de desenhar Δx muito pequeno, o gradiente Δy/Δx fica cada vez mais parecido com o gradiente real no ponto x = x0, e a reta tangente à curva de f no ponto x = x0 se torna visualmente “verdadeira”. É natural que pense assim: “Se eu pudesse desenhar um Δx infinitamente pequeno, o gradiente Δy/Δx se transformaria no gradiente real da reta que, de fato, tangencia f no ponto x = x0.”

Figura §57-5
Você não pode desenhar um intervalo Δx infinitamente pequeno; isso é impossível, pois a ponta de sua caneta é grossa demais. Mas pode imaginá-lo.
Definição §57-1. Considere a expressão a seguir.

Se y = f(x) é uma função definida em x = b, e se a expressão acima representa um hiper-real finito cuja parte padrão é a mesma qualquer que seja o infinitésimo ϖ que venha a escolher, positivo ou negativo, daí diga que f é diferenciável em b, e defina da maneira a seguir a derivada f’(b) da função f em x = b.

Em palavras: a derivada f’(b) da função f em x = b é o gradiente da reta tangente a f no ponto x = b, que você obtém ao pensar em Δx como um infinitésimo, isto é, quando faz x1 = b + ϖ para algum infinitésimo ϖ, positivo ou negativo. Com f’(b), portanto, você denota a taxa de variação instantânea da função f quando x = b. Da terceira à sétima linha no formulário acima, pode examinar várias maneiras pelas quais verá grafada a ideia de derivada de f em b. (Por exemplo, vai gostar da forma Df ao estudar álgebra linear; é uma notação que de fato simplifica as coisas quando trabalha com espaços vetoriais. A notação dy/dx é a de Leibniz, e é usada por muitíssimos autores.) Atenção a duas sutilezas: só deve falar da derivada de f em b se b é elemento do domínio de f; caso escolha dois valores distintos para ϖ e obtenha dois valores distintos para f’(b), daí por definição a derivada de f em b não existe, mesmo que b esteja no domínio de f.
Lembrete. Caso queira saber como pronunciar qualquer um dos símbolos para a derivada de f em b, diga: “A derivada de f em b”, “A derivada de y em relação a x”, ou “O coeficiente diferencial de f em b.”
* * *
Nas seções anteriores, já estudou as funções contínuas e provou vários teoremas sobre continuidade. Bem, os matemáticos descobriram que, se uma função f é diferenciável em b, é também contínua em b.
Teorema §57-1. Se f é uma função diferenciável em b, então é contínua em b.
Prova. Para todo infinitésimo ϖ, positivo ou negativo, [f(b + ϖ) – f(b)]/ϖ é um hiper-real finito; portanto, o dividendo 𝕯f(b) = f(b + ϖ) – f(b) tem de ser um infinitésimo ou zero, porque, se fosse um número real diferente de zero, [f(b + ϖ) – f(b)]/ϖ seria um hiper-real infinito. ❏
A recíproca desse teorema não é necessariamente verdadeira. Por exemplo, a função f(x) = |x| é contínua em zero, mas, como verá na seção 60 (uma lista de problemas), não pode diferenciá-la em zero. Eis a situação em que você se encontra quanto a funções diferenciáveis, contínuas, e integráveis:
Diferenciável implica contínua que implica integrável; contudo, integrável não implica contínua que não implica diferenciável.
Levou um par de séculos para que o homem provasse essa frase.
Definição §57-2. Se puder provar que f é diferenciável em todo ponto de um intervalo fechado [a, b], daí diga assim: “f é diferenciável em [a, b]”.
Note que, se f é diferenciável em [a, b], então você partiu de f e definiu uma nova função em [a, b], que é a função f’. Além disso, quando alguém te diz “a derivada de f”, talvez esteja querendo dizer “o coeficiente diferencial de f no ponto x = b” ou “a função derivada de f, que é a função f’, válida no intervalo [a, b]”. Cabe a você, a partir das circunstâncias, escolher o significado correto.
Sutileza. Como pode calcular a derivada de f em a se, para todo infinitésimo ϖ negativo, a + ϖ não faz parte do intervalo fechado [a, b]? E como pode calcular a derivada de f em b se, para todo infinitésimo ϖ positivo, b + ϖ não faz parte do intervalo fechado [a, b]? Simples: se pode calcular a derivada de f em a para todo infinitésimo positivo ϖ; se pode calcular a derivada de f em b para todo infinitésimo ϖ negativo; e se pode calcular a derivada de f no intervalo aberto (a, b) para todo infinitésimo ϖ, positivo ou negativo, daí f é diferenciável em [a, b]. Talvez alguém diga isso com estas palavras: “A funcão f é diferenciável em a pela direita, diferenciável em b pela esquerda, e diferenciável em (a, b) pela direita e pela esquerda.”

Figura §57-6: a função f está definida em a e b, embora tenha uma descontinuidade em a e b.
Antes de continuar, que tal uma pausa para calcular umas poucas derivadas? As ideias ficarão mais claras.

{58}/ Três exemplos
Exemplo 1. Ache a derivada da reta cuja equação é y = f(x) = mx + k no ponto em que x = x; nessa equação, m e k são dois números reais quaisquer.
Resolução. Trabalhe direto com a definição; escolha um infinitésimo ϖ qualquer, positivo ou negativo.

E com isso expressou, com a linguagem do cálculo diferencial, várias informações que já sabia de outros carnavais: (a) Num plano cartesiano XOY, o gradiente da reta y = ax + b equivale ao número real a, pois Dy = a; pode pôr essa ideia em palavras assim: “Em todo valor de x, a reta y = ax + b está crescendo à taxa de a unidades por unidade, se a é positivo, ou está diminuindo à taxa de a unidades por unidade, se a é negativo, ou não está nem crescendo nem diminuindo, se a é zero.” (b) O ângulo θ que a reta mx + k faz com o eixo X é θ = tan–1(Dy) = tan–1(m). (c) Toda função constante, do tipo y = f(x) = k para algum número real k, tem gradiente igual a zero, pois sua derivada Df é igual a zero, já que m = 0. (d) Note: se y = f(x) = mx + k, a função derivada f’(x) = m para todo x é uma função constante, cuja derivada é zero. Logo verá como conversar sobre a derivada de uma derivada, e como colocá-la no papel. (e) Visto que f é diferenciável para todo valor de x, é contínua em todo valor de x, como já provou antes no texto sobre continuidade (especialmente a seção 40).
Exemplo 2. Ache a derivada de f(x) = x2 em x = 1.
Resolução. Escolha um infinitésimo ϖ qualquer, positivo ou negativo, e vá direto para a definição.

Em palavras: quando x = 1, a função f está crescendo à taxa instantânea de 2 unidades por unidade. [Unidades no eixo Y por unidade no eixo X, sejam quais forem.] Se tivesse usado o eixo das ordenadas para marcar a distância em metros de certo corpo em relação a certo ponto de referência, e o eixo das abscissas para marcar o tempo em segundos, poderia dizer que, quando x = 1 segundo, o corpo está se afastando do ponto de referência à taxa instantânea de 2 metros por segundo, isto é, à velocidade de 2 metros por segundo. (A derivada da função posição, com a posição em relação ao tempo, se chama velocidade.)
Exemplo 3. Calcule a derivada de f(x) = 2x3 – 3x2 + 6x – 1 em x = 4.
Resolução. Escolha um ϖ qualquer, positivo ou negativo, e use as definições.

Em palavras: quando x = 4, a função f está crescendo à taxa de 78 unidades por unidade. Se usa f(x) para representar a quantidade de litros de combustível num reservatório, e x para representar a hora do dia, então com f’(4) está dizendo que, às 4 horas da manhã, alguém enchia o reservatório à taxa de 78 litros por hora.
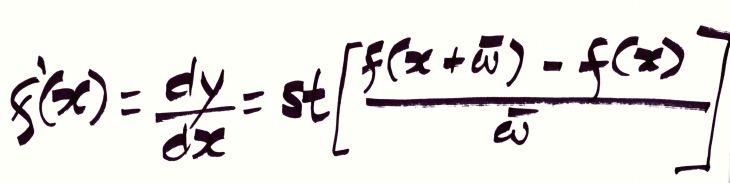
{59}/ As primeiras seis regras de derivação
Como talvez tenha notado com os três exemplos, é mais fácil achar a derivada de uma função que a integral. E isso quase sempre é verdade, embora algumas derivadas deem horas de trabalho. Nas linhas a seguir, verá seis teoremas bastante úteis no cálculo de derivadas. Procure compreender seu enunciado, parta do pressuposto de que são verdadeiros, e use-os para resolver a lista de problemas na seção 60. Vai provar os teoremas na seção 61, pois prová-los depois de tê-los usado é mais natural — é mais parecido com o que acontece em situações de pesquisa.
Teorema §59-1. “A regra da derivada de uma adição de funções.” Se f e g são duas funções diferenciáveis em x = b, e se h(x) = f(x) + g(x), daí h é diferenciável em b e h’(b) = f’(b) + g’(b).
Teorema §59-2. “A regra da derivada de um produto de funções.” Se f e g são duas funções diferenciáveis em x = b, e se h(x) = f(x)g(x), daí h é diferenciável em b e h’(b) = f’(b)g(b) + f(b)g’(b). (Com outra notação: Quando x = b, Dh = gDf + fDg.)
Teorema §59-3. “A regra da derivada do recíproco de uma função.” Se f é diferenciável em x = b e se f(b) ≠ 0, então a função h(x) = 1/f(x) também é diferenciável em b e, além disso:

O teorema a seguir é corolário dos teoremas §59-2 e §59-3.
Teorema §59-4. “A regra da derivada de um quociente de funções.” Se f e g são diferenciáveis em x = b e g(b) ≠ 0, daí a função h(x) = f(x)/g(x) é diferenciável em b e, além disso:

Teorema §59-5. “A regra da derivada de uma composição ou concatenação de funções — a regra da cadeia.” Se f é diferenciável em x = b e g é diferenciável em y = f(b), daí a função h(x) = g[f(x)] é diferenciável em b e, além disso:
![]()
Às vezes, o estudante expressa essa linha assim: “A derivada da função de fora vezes a derivada da função de dentro.” Evite o mnemônico, pois não se trata de “fora” ou “dentro”, mas sim de precedência: ao calcular o valor de h(x), você primeiro aplica a regra da função f a x, e depois aplica a regra da função g a f(x). Lembre-se de que pode escrever g[f(x)] = (g ◊ f)(x). Em todo caso, vai ouvir “fora” e “dentro” em todo lugar, visto que palavras não se submetem a decisões individuais.
Teorema §59-6. “A regra da derivada da parcela de um polinômio, ou ainda a regra da derivada de uma potência inteira de x.” Para todo inteiro positivo n, e para todo número real r, a derivada da função rxn equivale a nrxn–1. Veja como muita gente anota essa regra:

Com o apóstrofo, está dizendo ao leitor: “Ache a derivada da expressão dentro dos colchetes.” É um jeito conveniente de denotar a derivada de uma expressão matemática, e deve aprender a usá-lo.
(Devo dizer que “a derivada de uma expressão matemática” é significante, cujo significado é “a derivada da expressão que caracteriza uma função”?)

{60}/ Lista de problemas
§60-1. Se f(x) = x2 e a = 3, ache f’(a).
§60-2. Se f(x) = 5 – x2 e a = –1, ache f’(a).
§60-3. Se f(x) = x2 e a = 2, ache f’(a).
§60-4. Se f(x) = 2x4 – 3x2 + 1 e a = 0, ache f’(a).
§60-5. Prove que, se f e g são diferenciáveis em b, e se h(x) = f(x) – g(x), daí h é diferenciável em b e h’(b) = f’(b) – g’(b). (Se quiser, examine antes a prova do teorema §59-1.)
§60-6. Ache um exemplo de funções f e g tais que, se h = fg, então existe um x = b tal que h’(b) ≠ f’(b)g’(b).
§60-7. Se h(x) = kg(x), onde k é uma constante real e h, g são diferenciáveis em x = b, daí h’(b) = kg’(b). Use o teorema §59-2 para provar essa afirmação; por exemplo, comece com f(x) = k.
§60-8. Ache a derivada de f(x) = √x em qualquer ponto no qual x > 0.
§60-9. Se f(x) = x, ache f’(x), isto é, ache uma expressão para f’ que seja válida para todo valor de x.
§60-10. Se f(x) = x2, ache f’(x).
§60-11. Se f(x) = 7x2 – 2x + 3, ache f’(x).
§60-12. Se f(x) = x2√x, ache f’(x).
§60-13. Se f(x) = 1/x, ache f’(x).
§60-14. Se f(x) = x2/(3√x), ache f’(x).
§60-15. Se f(x) = senx, ache f’(x). (Esse é difícil; depois de tentar, pesquise na internet.)
§60-16. Se f(x) = cosx, ache f’(x).
§60-17. Se f(x) = tanx, ache f’(x).
§60-18. Se f(x) = secx, ache f’(x).
§60-19. Se f(x) = cotx, ache f’(x).
§60-20. Se f(x) = cscx, ache f’(x).
§60-21. Se f(x) = senx2, ache f’(x). (Use a regra da cadeia, com y = h(x) = x2 e g(y) = seny.)
§60-22. Diferencie (x + 3)2.
§60-23. Diferencie √(x2 + 7).
§60-24. Diferencie 1/√x.
§60-25. Calcule [√x]’, mas desta vez use a regra da cadeia; faça g(x) = x2.
§60-26. Prove que f(x) = |x| é contínua em x = 0.
§60-27. Prove que, embora f(x) = |x| seja contínua em x = 0, não pode diferenciá-la em x = 0.
Sugestões de resposta na seção 69.
![]()
{61}/ A prova dos seis teoremas
Prova do teorema §59-1. Se h(x) = f(x) + g(x), escolha um infinitésimo ϖ qualquer, positivo ou negativo, e daí, usando as definições:

Ao derivar funções polinomiais, portanto, pode derivar cada uma das parcelas separadamente; a derivada da função será a soma das derivadas.
Prova do teorema §59-2. Escolha um infinitésimo ϖ qualquer, positivo ou negativo, e use as definições.

Mas, se adicionar f(b) a f(b + ϖ) e depois tirar f(b) de f(b + ϖ), permanece com f(b + ϖ). Logo, pode reescrever f(b + ϖ) e g(b + ϖ) assim:

Use essa informação para retomar a sequência anterior.

Por um tempo, Leibniz acreditou que h’(b) = f’(b)g’(b), que é uma expressão mais limpa e bonita. Não demorou muito para perceber que, nesse caso, boniteza não punha o pão na mesa, pois as contas não davam certo. Atacou o problema outras vezes, de várias maneiras, mas precisou de uns poucos anos até resolvê-lo em definitivo. Isso mesmo: anos!
Prova do teorema §59-3. Escolha um infinitésimo ϖ qualquer, positivo ou negativo. Daí, se f é diferenciável em b e se f(b) ≠ 0:

Deve ter notado que está usando bastante os teoremas da seção 22. Se julgar necessário, estude essa seção mais uma vez.
Prova do teorema §59-4. O que deve fazer neste caso é simplesmente usar os teoremas §59-2 e §59-3; basta que veja h como um produto de funções: h(x) = f(x) · [1/g(x)].

Prova do teorema §59-5. Quando você vê a prova deste teorema pela primeira vez, não entende muito; depois se esforça e entende. Uns meses depois, quando vê a prova pela segunda vez, a história se repete. E talvez se repita mais algumas vezes. Ora, se é difícil entender a prova desse teorema, imagine o trabalho danado que deve ter sido prová-lo pela primeira vez. (O mérito é atribuído a Leibniz, que certamente produziu uma prova sozinho, mas historiadores ainda discutem a primazia.)
Comece escolhendo um infinitésimo ϖ, positivo ou negativo. E vá direto para a definição da derivada de h no ponto em que x = b:

Tem de tomar cuidado aqui, pois a expressão é quase igual à que viu na definição §57-1, com esta diferença: o infinitésimo que usou no dividendo, que é 𝕯f, não é o mesmo que usou no divisor, que é ϖ. É por isso que deve manejar a expressão da última linha com extremo cuidado.
Do teorema §57-1, f é contínua em x = b, e por isso 𝕯f ou é um infinitésimo ou é zero. [A ideia é que f(b + ϖ) ≈ f(b), visto que f é contínua em b, e por isso a diferença entre ambos ou é um infinitésimo ou é zero.]
Antes de continuar, precisa compreender um ponto: pode ver 𝕯h(b) = 𝕯g[f(b)]. Veja o porquê:

Voltando. Suponha que 𝕯f é zero; então 𝕯h também é, e assim escreva:

Uma coisa boa do zero é que você pode transformá-lo na expressão que bem entender, pois qualquer coisa vezes zero é zero.
Suponha agora que 𝕯f é um infinitésimo positivo ou negativo, mas não nulo. Visto que 𝕯h = 𝕯g, você obtém:

QED.
Muita gente precisa de ajuda para ver o que aconteceu na passagem da quarta para a quinta linha, e talvez esse seja seu caso. Faça, como antes, 𝕯f(b)= f(b + ϖ) – f(b) e, além disso, faça também f(b) = u. Daí substitua:

Professores dizem que muito estudante só entende uma demonstração como essa se recorre ao truque de substituir variáveis, como fez com f(b) = u. Fica a dica.
Prova do teorema §59-6. O jeito mais simples de provar esse teorema é recorrer ao teorema binomial. (Do qual há várias boas provas na internet.) Por meio dele, você pode dizer: as linhas a seguir, nas quais x e y são números reais, são válidas para todo n inteiro positivo.

Escolha um infinitésimo ϖ, positivo ou negativo, parta do pressuposto de que o teorema binomial é válido, e use as definições para y = f(x) = rxn. Veja o que obtém:

Como pode justificar a implicação na última linha? Bem, neste caso f é uma função polinomial — e você pode definir uma função polinomial para todo valor real de x. (O domínio de f é ℝ.) Visto que a derivada de f também é uma função polinomial, também pode defini-la para todo valor real de b, inclusive b = x.
Segunda prova do teorema §59-6. Eis uma prova por contradição, na qual você não precisa invocar o teorema binomial.
Suponha que o teorema §59-6 é falso. Daí, para algum valor inteiro positivo de n, a derivada de rxn não é nrxn–1. Chame de k o menor de tais valores de n, isto é, a derivada de rxk não é krxk–1, mas a derivada de rxk-1 é (k – 1)rxk–2. Com o que viu na seção 57, já sabe que k > 1, pois já provou que o teorema é válido para k = 0 [se f(x) = r, f’(x) = 0, que é 0 · r · x0–1] e para k = 1 [se f(x) = rx, f’(x) = r, que é 1 · r · x1–1]. Daí k – 1 < k, e o teorema tem de ser válido para rxk–1, de modo que a derivada de rxk–1 é (k – 1)rxk–2. Use então essa informação, pois, se faz g(x) = rxk–1 e h(x) = x, tem como invocar o teorema §59-2 e escrever:

Visto que a última linha contradiz a pressuposição inicial (“o teorema §59-6 é falso”), então deve dizer que a negação da pressuposição inicial é verdadeira: “O teorema §59-6 é verdadeiro.”
Exercício §61-1. Prove que, para x ≠ 0 e n inteiro positivo, a derivada de rx–n é –nrx–n–1. Dica: faça x–n = 1/xn e use os teoremas §59-3 e §59-6. Depois compare sua prova com a sugestão na seção 69.

{62}/ Máximos, mínimos, e valores médios
É hora de estudar a prova de dois teoremas importantes no cálculo: [1] o teorema da derivada igual a zero em máximos ou mínimos; e [2] o teorema do valor médio. São dois teoremas difíceis, mas vale a pena estudá-los à exaustão.
Engenheiros e especialistas em matemática aplicada usam o primeiro teorema numa quantidade muito grande de problemas práticos e teóricos. Quanto ao segundo teorema (que é, na verdade, um corolário do primeiro), matemáticos usam-no como ponto de partida para a prova de mais de uma dúzia de teoremas importantes, entre eles:
1. O teorema de Taylor. É uma generalização do teorema do valor médio, com a qual você demonstra como pode calcular o valor aproximado de uma função (com erro de aproximação tão pequeno quanto deseje) por meio de polinômios infinitos.
2. Uma generalização diferente do teorema do valor médio, escrita por Cauchy, com a qual demonstra a regra de L’Hospital.
3. Uma terceira generalização, com a qual define bem precisamente a enésima derivada de uma função para qualquer inteiro positivo n.
4. O teorema com o qual responde à questão: “Se f’(x) é zero para todo valor de x, será que f(x) é constante?”
5. Metade da prova do teorema fundamental do cálculo, que você vai estudar no próximo capítulo desta série.
6. O teorema de Darboux.
7. O teorema com o qual você descreve, muito sucintamente, as funções f que têm função derivada f’ contínua.
* * *
Pense no seguinte problema: a função y = f(x) = x3 + 2x2 + x + 1 é contínua no intervalo [–3/4, –1/4]. Examine agora uma plotagem da curva de f nesse intervalo:

Figura §62-1
Basta inspecionar a figura §62-1 para ver que a curva de f atinge um mínimo; de fato, como já viu ao provar o teorema §31-2, f tem de assumir um mínimo em algum valor de x entre x = –3/4 e x = –1/4.
Problema. Ache o valor de x no qual f atinge um mínimo nesse intervalo.
Tente propor um problema como esse para um estudante que já sabe mexer com polinômios, mas que ainda não sabe nada sobre cálculo, e veja como se debate — pois, sem o cálculo, o problema é difícil. Para você, contudo, é bem mais fácil: visto que f é uma função polinomial, e assim derivável em toda parte, a curva de f assume um mínimo num ponto em que sua derivada f’ vale zero, isto é, num ponto em que o gradiente é zero.

Figura §62-2
Ora, com o que já sabe, use o teorema §59-6 para calcular de cabeça a derivada de f:
![]()
Iguale f’(x) a zero e, com Bháskara, ache as duas raízes da equação.

Desses dois pontos, apenas x = –1/3 faz parte do intervalo [–3/4, –1/4], de modo que (–1/3, 23/27) é o ponto na curva de f na qual f atinge o menor valor no intervalo [–3/4, –1/4]. Esse método não parece natural?
Matemáticos como Leibniz, Newton, Taylor, e Fermat usaram essa ideia (num máximo ou mínimo, a derivada de uma função derivável tem de ser zero) muito antes que alguém pudesse prová-la para além de qualquer dúvida, o que aconteceu uns 200 anos depois. É o que você vai provar agora.
Teorema §62-1. “Teorema dos máximos ou mínimos.” Presuma que y = f(x) é uma função diferenciável no intervalo aberto (a, b), e que, num ponto c pertencente a (a, b), f assume um máximo ou um mínimo. Daí f’(c) = 0.
Prova. Primeiro, presuma que f(c) é um máximo. Visto que f(c) é um máximo, pode declarar como válida a linha a seguir, na qual ϖ é um infinitésimo positivo ou negativo.
![]()
Pense agora em ϖ como um infinitésimo positivo, de modo que a figura §62-2 e a expressão no formulário a seguir sejam válidas.

Formulário §62-1

Figura §62-2
Uma pausa para entender por que a expressão é válida. Bem, [f(c – ϖ) – f(c)]/ϖ é ≤ 0, pois f(c) é um máximo e ϖ é positivo. Só que [f(c – ϖ) – f(c)]/ϖ não corresponde à definição de derivada, pois está usando um infinitésimo no dividendo, que é –ϖ, e outro no divisor, que é ϖ. Para corrigir isso, multiplique o infinitésimo no divisor por –1; daí obtém uma expressão condizente com a definição de derivada, mas com o sinal trocado, isto é, obtém uma expressão ≥ 0.
Continuando:
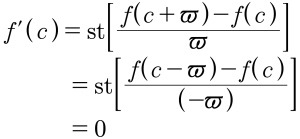
Para ver por que isso é verdade, multiplique toda a expressão no formulário §62-1 por ϖ e depois por –1 (o que inverte as desigualdades); fica com f(c) – f(c + ϖ) ≥ 0 ≥ f(c – ϖ) – f(c), isto é, fica com o zero entre dois hiper-reais; cada um deles ou é um infinitésimo ou é zero, conforme o formato da curva. Visto que f é diferenciável, por definição sabe que, ao dividir os os dois infinitésimos por ϖ, vai obter o mesmo número hiper-real — só que com o sinal trocado. Daí o valor padrão das duas expressões é o único número real infinitamente próximo das duas expressões na desigualdade acima deste parágrafo, e esse número só pode ser zero. Por meio de um argumento similar, você prova o caso em que f(c) é um mínimo, e com isso prova o teorema.
Teorema §62-2. “Teorema do valor médio.” Presuma que f(x) é diferenciável no intervalo aberto (a, b). Daí, para algum c em (a, b), a expressão a seguir é verdadeira.

Prova. Esse teorema é, no fundo, uma versão rotacionada do teorema anterior, como vê na figura §62-3.


Figura §62-3: A curva de baixo é uma versão rotacionada da curva de cima.
Note que a expressão a seguir é o gradiente da reta secante AB.

Se você, na imaginação, rotaciona a curva de f, de modo que a reta AB se confunda com o eixo X (como vê na figura §62-3), daí o que deve procurar é um número real c tal que R’(c) = 0 na função rotacionada R(x). [Na verdade, para ser preciso, na transformação R : f(x) ↦ R(x); nada garante que, com a rotação, você continuará tendo uma função, já talvez um elemento do domínio passe a levar a mais de um elemento na imagem, mas certamente terá uma transformação diferenciável.] Daí, pelo teorema §62-1, esse número c será parte de um ponto em (a, b) onde R assume um máximo ou um mínimo.
Então, o que deve fazer é deixar essa ideia bem precisa. Dada a função f(x), defina R(x) assim:

Note que a derivada de R é:

Sabe isso graças ao teorema §59-1 e ao exemplo que estudou na seção 57. Assim, diga que R é a versão rotacionada de f. Faça c um ponto no qual R assume um máximo ou um mínimo. Se a < c < b, o teorema anterior diz que R’(c) = 0, isto é, diz o seguinte:

Agora, caso tanto o máximo quanto o mínimo de R(x) ocorram nos pontos extremos a e b, veja o que acontece:

Isso quer dizer que o valor máximo de R é igual ao valor mínimo em [a, b], de modo que R tem de ser uma função constante em [a, b], como pode ver na figura a seguir.

Figura §62-4
Mas, se for assim, daí R’(c) = 0 para qualquer c no intervalo aberto (a, b). Em qualquer um desses casos, declare como válida a expressão a seguir:

E com isso o teorema está provado.
Esses dois teoremas têm três aplicações interessantes, que formam, de fato, um corolário deles dois.
Corolário §62-1. Presuma que f é diferenciável em [a, b]. Daí:
(1) Se f’(x) = 0 para todo x em [a, b], f é constante.
(2) Se f’(x) > 0 para todo x em [a, b], f é monótona, estritamente crescente, e nunca é constante.
(3) Se f’(x) < 0 para todo x em [a, b], f é monótona, estritamente decrescente, e nunca é constante.
Prova. Pense em dois números c, d do intervalo [a, b], com c < d. Pelo teorema do valor médio, existe um número q entre c e d tal que:

Logo, f’(q)(d – c) = f(d) – f(c). Se f’(x) é sempre zero, daí f(d) – f(c) é sempre zero, isto é, f(d) = f(c) para quaisquer dois desses números c, d em [a, b]. Com isso, você prova a afirmação (1). Note que a afirmação (1) é a recíproca de outra que já provou na seção 58: se f é uma função diferenciável e f(x) = k para todo x no domínio de f, daí f’(x) = 0.
Se f’(x) é sempre positiva, daí f(d) – f(c) > 0 e f(d) > f(c). Com isso, prova a (2).
Por fim, se f’(x) é sempre negativa, daí f(d) – f(c) < 0 e f(d) < f(c). Com isso, prova a (3).

{63}/ Lista de problemas
§63-1. Estude a função f(x) = x|x|. (a) Prove que, para x > 0, f’(x) = 2x. (b) Prove que, para x < 0, f’(x) = –2x. (c) Prove que f’(0) = 0.
§63-2. Prove que não pode derivar f(x) = 2|x| em x = 0.
Definição §63-1. “Como denotar a enésima derivada de uma função.” Dada uma função diferenciável f, talvez sua função derivada f’ também seja diferenciável. E dada uma função diferenciável f’, talvez sua função derivada f’’ também seja diferenciável. Em casos assim, pode denotar a segunda derivada de f com f’’ ou f(2); a terceira derivada de f com f’’’ ou f(3); e a enésima derivada de f com f(n). Além disso, usando notação de Leibniz:
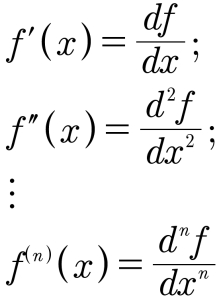
§63-3. Se h(x) = f(x)g(x) é uma função infinitamente diferenciável, parta do teorema §59-2 e proponha uma expressão para h(n)(x); use indução matemática para prová-la correta. (Se Leibniz conseguiu, você também consegue.)
§63-4. Você tem diante de si o gráfico da parábola y = f(x) = ax2 + bx + c, expressão na qual a, b, c são coeficientes reais, com a ≠ 0. Como pode produzir a fórmula com a qual calcular as coordenadas do vértice da parábola?
§63-5. Em várias das demonstrações até aqui, você pensou num intervalo aberto (a, b), e destacou um número c desse intervalo. Para algum infinitésimo ϖ, positivo ou negativo, explique mais uma vez por que c + ϖ faz parte do intervalo.
§63-6. Presuma que a função f(x) = logx está bem definida e tem uma função derivada f’(x). Como poderia provar que f’(x) = k/x para alguma constante k? (Esse é difícil; tente resolvê-lo sozinho, e depois pesquise na internet.)
§63-7. Considere a função a seguir:

(a) Prove que f é descontínua para todo x ≠ 0. (b) Prove, contudo, que f é diferenciável em x = 0.

{64}/ Yoda: “De uma função derivável, nem sempre a derivada derivável é.”
A função a seguir está entre os exemplos mais simples de uma função diferenciável em toda parte, mas cuja função derivada, embora esteja definida para todo valor de x, é descontínua, isto é, não é diferenciável em toda parte.

Usando os teoremas: x2, senx são diferenciáveis para todo valor de x, e 1/x é diferenciável para todo valor de x ≠ 0. Logo, sen(1/x), que é uma concatenação de funções, é diferenciável para todo x ≠ 0, e x2sen(1/x), que é um produto de funções, também é diferenciável para todo x ≠ 0.
Como pode descobrir o comportamento de f quando x = 0? Use a definição de derivada; nas linhas a seguir, ϖ é um infinitésimo positivo ou negativo.
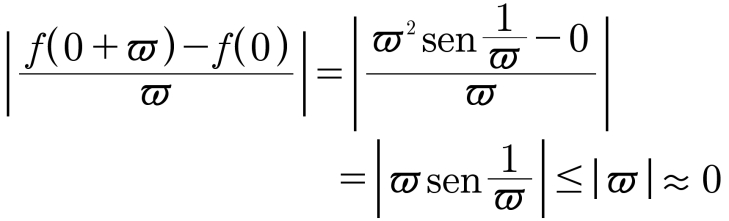
Diga que a última linha vale porque –1 ≤ sen(1/ϖ) ≤ 1, e quando você multiplica um número hiper-real finito por um infinitésimo, obtém um infinitésimo. Além disso, visto que a última linha vale para qualquer infinitésimo ϖ, positivo ou negativo, daí escreva:

Já pode calcular a expressão completa para a função derivada f’.

É hora de provar que a função f’ acima é descontínua em x = 0. Já fez algo parecido com isso ao resolver o problema §32-2. Se pensa em N como um hiper-real inteiro infinito, sabe que sen0 = 0, logo sen(0 + 2πN) = sen(2πN) = 0; além disso, cos0 = 1, logo cos(0 + 2πN) = cos(2πN) = 1. Faça daí ϖ = 1/(2πN). Explore a consequência lógica de tais decisões:

Se f’ fosse contínua em x = 0, para todo hiper-real ϖ infinitamente próximo de 0, f’(ϖ) deveria estar infinitamente próximo de f’(0). Mas, como viu, se faz ϖ = 1/(2πN), daí ϖ ≈ 0, mas f’(0) = 0 ≉ f’(ϖ) = –1, e com isso prova que, embora possa derivar f para todo valor de x, e embora a função derivada f’ esteja definida para todo valor de x, não tem como derivar f’ para todo valor de x, pois é descontínua em x = 0.
Em palavras: “Nem sempre a função derivada de uma função derivável é derivável.” O jeito Yoda de dizer isso é bem mais legal.
O teorema de Darboux, que não vai estudar aqui, diz o seguinte: “Se f é diferenciável, então f’ tem a propriedade de Darboux.” Lembrete: se uma função g tem a propriedade de Darboux no intervalo fechado [a, b], os elementos da imagem assumem todos os valores entre g(a) e g(b). Portanto, se f é diferenciável em [a, b], o máximo que você pode dizer de f’ é que assume todos os valores entre f’(a) e f’(b), já que f’ talvez não seja diferenciável, e talvez nem mesmo seja contínua.

{65}/ A aplicação clássica: distância e velocidade
Você sempre usa a ideia de derivada, mesmo que não perceba, quando fala de velocidade. Imagine um carro que percorre uma estrada reta. A certa altura, você estabelece um ponto de referência O, e passa a medir a distância do carro até O conforme o tempo, de modo que, dado um tempo t, a distância do carro até O é s(t). Se plotar isso num gráfico da distância pelo tempo, terá algo mais ou menos como a figura §65-1 a seguir.

Figura §65-1
Com o gráfico, está mostrando a seu leitor que o carro se afasta e se aproxima de O conforme vai e vem pela estrada reta.
Daí, em determinado t = t0, qual é a velocidade do carro?
Como já viu na seção 42, é bem provável que a velocidade do carro varie o tempo todo, talvez aos trancos e barrancos, talvez suavemente. Assim, você não pode simplesmente pegar um outro tempo t = t1 e calcular a velocidade média do carro no intervalo de tempo t1 – t0:

Veja agora o gráfico na figura §65-2. Se a expressão acima é igual à velocidade média, também é igual ao gradiente da reta secante PQ, e, como o gráfico deixa claro, talvez a velocidade média não seja igual à velocidade instantânea em t0, e talvez ainda seja muito diferente.

Figura §65-2
Agora, se fizer o tempo t1 infinitamente próximo de t0, de modo que a velocidade média esteja infinitamente próxima da velocidade instantânea em t0, daí você pode calcular a velocidade do carro em t0 assim:

Em palavras: a velocidade instantânea em t0 é a derivada da função posição s(t) em t = t0. Físicos dizem isso mais simplesmente: “A derivada da posição é a velocidade.” Essa ideia faz todo o sentido: se você mede a posição em quilômetros, e o tempo em horas, a unidade de s’(t) será em quilômetros por hora, pois uma derivada é sempre no formato “unidades no eixo das ordenadas por unidade no eixo das abscissas”. Se a derivada s’(t0) = 0, isto é, se a velocidade é zero quando t = t0, o carro não está mudando de posição — não está indo a lugar nenhum, como convém a um carro cuja velocidade é zero.
Em tempo: A derivada da velocidade é a aceleração, e a derivada da aceleração é a arrancada. Em inglês, arrancada é jerk, que também significa “idiota” ou “babaca”. Por isso as camisetas onde se lê:
Don’t be a a’(t).

{66}/ O quebra-cabeça das funções inversas
Os teoremas §62-1 e §62-2, e o corolário §62-1 têm outro corolário importante:
Corolário §66-1. “O teorema da função inversa.” Suponha que f é diferenciável e que ou f’(x) > 0 no intervalo fechado [a, b], ou f’(x) < 0 em [a, b]. Daí f tem uma função contínua inversa g, que você pode definir perfeitamente entre f(a) e f(b); além disso, para todo y = f(x) nesse intervalo:

Lembrete 1: Das aulas de geometria analítica, sabe que g é função inversa de f se, para todo x no domínio de f, f(x) = y implica g(y) = x, isto é, f(g(y)) = y e g(f(x)) = x para todo x e y nos conjuntos domínio e imagem apropriados.
Lembrete 2: Se f’(x) > 0 em [a, b], f é estritamente crescente em [a, b]; e se f’(x) < 0 em [a, b], f é estritamente decrescente em [a, b].
Prova do corolário. Pelo teorema §57-1, f é contínua. Assim, para todo y entre f(a) e f(b), pelo teorema do valor intermediário existe no mínimo um x entre a e b tal que f(x) = y. Visto que f nunca é constante pelo corolário §62-1, existe então só um valor de x tal que f(x) = y. Defina g(y) como sendo esse valor único de x, isto é, x = g(y). Com tal definição, você tem:
![]()
Logo, diga que g é sem dúvida a inversa de f. [Usando uma notação bastante comum: g = f–1.]
Para demonstrar que g é uma função contínua, suponha que y é um número real qualquer entre f(a) e f(b), e que h é um hiper-real infinitamente próximo de y, isto é, h ≈ y. Daí, se g(h) ≉ g(y), tem de existir um número real r entre x = g(y) e q = g(h). Daí f(r) é um número real entre y = f(g(y)) e h = f(g(h)), pois f é monótona. Mas, dado que y ≈ h, não pode haver um número real entre y e h. Assim, não pode haver um número real entre g(y) e g(h), de modo que g(y) ≈ g(h), e com isso você prova que g é contínua.
Por fim, para descobrir uma expressão para g’(y), comece com um infinitésimo ϖ qualquer, positivo ou negativo. Faça x = g(y), e portanto faça y = f(x); depois disso, faça ϖ2 = g(y + ϖ) – g(y). Visto que g é contínua, ϖ2 também é um infinitésimo. Daí eis o que obtém:

E com isso você conclui a prova.
Ao trabalhar com gráficos, você obtém a curva inversa da curva de f ao usar a linha reta y = x para refletir a curva de f; pense na linha y = x como a linha de um espelho. Para fazer isso, eis o método: correlacione cada ponto P = (x, f(x)) na curva de f com o ponto P’ = (f(x), x) na curva g inversa de f. Fazendo isso, o segmento de reta PP’ fica perpendicular à linha reta y = x, e a linha reta y = x intercepta o segmento PP’ bem no ponto médio. É o que pode ver na figura §66-1 a seguir. Por esse método, fica fácil entender por que, se a curva de f é contínua, a curva inversa de f também é.

Figura §66-1

{67}/ Lista de problemas
§67-1. Verifique se x2 e √y são funções inversas.
§67-2. Verifique se 2x – 5 e (1/2)(y + 5) são funções inversas.
§67-3. Verifique se 10x e log10y são funções inversas.
§67-4. Verifique se xn e y(1/n) são funções inversas.
§67-5. Ache a inversa de x + 7.
§67-6. Ache a inversa de 3x – 1.
§67-7. Ache a inversa de x3.
§67-8. Ache a inversa de x√x.
§67-9. Use o problema §67-4 para provar que a derivada de g(y) = y(1/n) é g’(y) = (1/n)y(1/n)–1.
§67-10. Use o problema §67-9 e os teoremas §59-5 e §59-6 para provar que a derivada de xn/m é (n/m)x(n/m)–1. (É preciso dizer que n, m são inteiros, com m ≠ 0?)
Observação sobre o problema a seguir (§67-11): No intervalo aberto (0, π), a derivada de y = f(x) = cosx é negativa, e portanto cosx tem uma função inversa, que em geral o matemático denota com x = g(y) = arccosy ou x = g(y) = cos–1y. Usando o teorema da função inversa, eis o que pode descobrir:

§67-11. Ache um intervalo no qual existe a função inversa de senx, e calcule a derivada de sen–1y.
§67-12. Ache um intervalo no qual existe a função inversa de tanx, e calcule a derivada de tan–1y.
Sugestões de resposta na seção 69.

{68}/ A equação da reta tangente
Eis uma pergunta importante, pois vai usar a resposta numa quantidade enorme de situações práticas: Qual é a equação completa da reta tangente a f no ponto x = b? (Supondo, é claro, que f seja diferenciável em b.) Pode ver na figura §68-1 o que está procurando.

Figura §68-1
Chame a linha reta que está procurando de g. Logo, a equação completa da reta tangente a f no ponto b é:
![]()
Quando x = b, f(b) = g(b); use essa informação para calcular o valor de C.

Com isso, ponha no papel a equação completa da reta g tangente a f no ponto x = b.

Às vezes, o matemático se refere à função g com as palavras “a linearização de f em b”. Eis uma aplicação simples e útil da linearização de f em b:
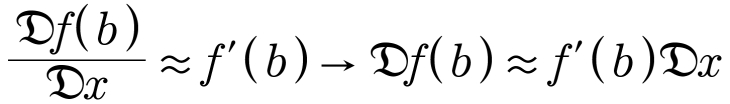
Olhe a figura §68-2 para entender melhor a utilidade dessa aplicação: se gostaria de saber como f se comporta logo à direita ou logo à esquerda de b (está pensando em b ± Δx para algum Δx positivo), basta que multiplique f’(b) por ±Δx. Obterá uma estimativa próxima da variação verdadeira Δf = f(b ± Δx) – f(b), e quanto menor o valor que atribui a Δx, mais próxima fica a estimativa da variação verdadeira.

Figura §68-2
Isso significa que, se sabe posição e a velocidade de um foguete no tempo x = b, multiplique a velocidade por um Δx bem pequeno, tipo 1 segundo, e terá boa ideia da posição do foguete 1 segundo depois de b.
Lembrete. Com b ± Δx, você denota duas expressões: b + Δx ou b – Δx. Aliás, se quiser, pode pronunciar b ± Δx assim: “Bê mais delta xis ou bê menos delta xis.” Atenção à palavra “ou”. Se diz que b ± Δx é a solução de uma equação, diz que tanto b + Δx sozinha quanto b – Δx sozinha resolve a equação. Se usasse a palavra “e”, o que é um erro, estaria dizendo que, para resolver a equação, precisa ao mesmo tempo de b + Δx e também de b – Δx.
* * *
Tangentes verticais. Considere a curva de y = f(x) = 5√(2 – x); é a que vê na figura §68-3 mais abaixo. A derivada f’ de f é:

Bem, f’(2) não existe, pois não se pode dividir nada por zero. Mas, caso faça x = 2 + ϖ para algum infinitésimo ϖ negativo, daí x ≈ 2 e, além disso:

Nessa expressão, com –N você denota um hiper-real negativo infinito. Numa sala de aula comum, o professor diria que, quando x tende a 2 pela esquerda, a expressão de f’(x) tende ao infinito negativo, e neste caso isso significa que a derivada de f não existe. [Quanto a você, que conhece o sistema dos números hiper-reais, diga que não pode atribuir um valor real a um hiper-real infinito, e portanto não pode atribuir um valor real a f’(2).]
Isso não significa que não existe uma reta tangente a f no ponto x = 2, pois ela existe: é a reta vertical x = 2.

Figura §68-3
Como vê, deve tomar esse cuidado: se verifica que x = b pertence ao domínio de f, mas ao calcular 𝕯f(b)/𝕯x obtém um hiper-real infinito, quase sempre é porque a reta tangente a f em b é vertical. (Existem outros casos, mas são assunto para outro dia.)
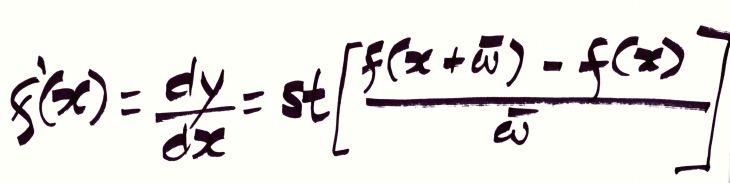
{69}/ A resolução dos problemas
Em todas as resoluções a seguir, ϖ denota um infinitésimo positivo ou negativo — a não ser que o redator dê aviso em contrário.
§60-1. Se f(x) = x2 e a = 3, ache f’(a).
Resolução. Eis como devem ficar suas contas:

Em palavras: quando x = 3, f está crescendo à taxa instantânea de 6 unidades por unidade.
§60-2. Se f(x) = 5 – x2 e a = –1, ache f’(a).
Resolução. De uma vez:

§60-3. Se f(x) = x2 e a = 2, ache f’(a).
Resolução. As notas são:

Em palavras: quando x = 2, f está crescendo à taxa instantânea de 4 unidades por unidade.
§60-4. Se f(x) = 2x4 – 3x2 + 1 e a = 0, ache f’(a).
Resolução. Use a definição de derivada e tome cuidado com as contas.

Veja no gráfico a seguir como f atinge um máximo local quando x = 0. (Máximo local é um máximo no entorno daquele local, e não um máximo global, isto é, o maior valor que f possa atingir.)

Em palavras: quando x = 0, f não está nem crescendo nem decrescendo.
§60-5. Prove que, se f e g são diferenciáveis em b, e se h(x) = f(x) – g(x), daí h é diferenciável em b e h’(b) = f’(b) – g’(b).
Resolução. O que deve fazer é usar as definições com cuidado e paciência:

Da terceira para a quarta linha, o que fez foi multiplicar o quociente à direita por (–1)/(–1); isso é a mesma coisa que multiplicá-lo por 1, e não altera seu valor.
§60-6. Ache um exemplo de funções f e g tais que, se h = fg, então existe um x = b tal que h’(b) ≠ f’(b)g’(b).
Resolução. Não precisa ir longe: faça f(x) = x e g(x) = x2. Agora, se h(x) = f(x)g(x), e se fosse o caso de que h’(x) = f’(x)g’(x), daí h’(x) = 1 · 2x = 2x. Mas h(x) = x3, e pelo teorema §59-6 h’(x) deveria valer 3x2.
Com a regra do produto de duas funções (teorema §59-2), contudo, você obtém o resultado correto:

§60-7. Se h(x) = kg(x), onde k é uma constante real e h, g são diferenciáveis em x = b, daí h’(b) = kg’(b).
Resolução. Faça f(x) = k, e h(x) = f(x)g(x). Daí aplique o teorema §59-2: h’(b) = f’(b)g(b) + f(b)g’(b). Ao estudar o exemplo 1, já viu que f’(x) = 0 para todo valor de x. Logo, h’(b) = f(b)g’(b) = kg’(b).
§60-8. Ache a derivada de f(x) = √x em qualquer ponto no qual x > 0.
Resolução. Use as definições e o que sabe de álgebra.

Com isso, você não apenas prova que, para todo x > 0, [√x]’ = 1/(2√x); você também prova que √x é diferenciável para todo x positivo.
Talvez tenha notado uma coincidência. Faça f(x) = √x = x(1/2) e aplique a f o teorema §59-6 como se pudesse aplicá-lo a expoentes fracionários.
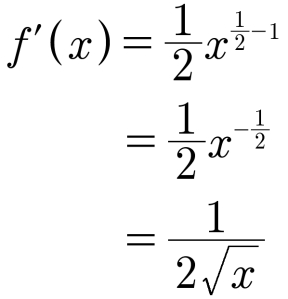
Quando resolver o problema §67-9, verá que isso não é mera coincidência.
§60-9. Se f(x) = x, ache f’(x).
Resolução. Faça x = x1 e aplique o teorema §59-6: [x1]’ = 1 · x(1–1) = 1 · x0 = 1 · 1 = 1. (Pode aplicar o teorema porque tem como definir f para todo valor de x.) Se aplicasse a definição de derivada para x = x chegaria ao mesmo resultado:

Aplicar um teorema é quase sempre mais fácil que aplicar a definição de derivada desde o comecinho.
§60-10. Se f(x) = x2, ache f’(x).
Resolução. Já sabe que pode definir f para todo valor de x. Aplique mais uma vez o teorema §59-6: f’(x) = 2x(2–1) = 2x. Logo, [x2]’ = 2x. Talvez queira provar esse resultado não com o teorema, mas a partir da definição de derivada.

Atenção a uma sutileza: quando aplica a definição de derivada, está provando que pode derivar f(x) = x2 para todo valor de x. Quando aplica o teorema §59-6, mas sem antes provar que f é derivável para todo valor de x, está partindo do pressuposto de que f é derivável para todo valor de x. Cuidado. Nem sempre é o caso.
§60-11. Se f(x) = 7x2 – 2x + 3, ache f’(x).
Resolução. Você sabe que pode derivar cada uma das parcelas do polinômio em todo valor de x. É tão fácil recorrer ao teorema da derivada de uma adição de funções (§59-1) e ao teorema da derivada de uma potência de x (§59-6):

Note que, se quiser, também pode derivar a última parcela com o teorema §59-6: faça 3 = 3x0; daí [3]’ = [3x0]’ = 0 · 3 · x(0–1) = 0.
§60-12. Se f(x) = x2√x, ache f’(x).
Resolução. Com o problema §60-8, você descobriu que [√x]’ = 1/(2√x). Com o problema §60-10, viu que pode derivar x2 em todo valor de x. Sabendo isso, só precisa usar o teorema sobre a derivada de um produto de funções:

Um problema: para que a segunda linha seja válida, x tem de ser maior que zero. Pode resolvê-lo com facilidade: diga que, se x > 0, [x2√x]’ = (5/2)x√x. Notou a diferença entre “a verdadeira derivada” e “uma expressão arrumadinha para a verdadeira derivada”?
§60-13. Se f(x) = 1/x, ache f’(x).
Resolução. Com o exemplo 1, já viu que pode diferenciar a função y = x em todo valor de x; além disso, se x ≠ 0, então 1/x ≠ 0. Agora basta usar o teorema §59-3 sobre o recíproco de uma função.

Em outras palavras, se x ≠ 0, f(x) = 1/x implica f’(x) = –x–2. Presuma agora que, se quisesse, poderia ter usado o teorema §59-6 sobre a derivada de uma potência de x, só que uma potência negativa. Daí [x–1]’ = –1 · x–1–1 = –x–2. Se já resolveu o exercício §61-1, deve ter visto que isso não é mera coincidência.
§60-14. Se f(x) = x2/(3√x), ache f’(x).
Resolução. Com o que viu nos problemas anteriores e nos exemplos do texto, sabe que pode diferenciar x2 e 3√x em todo valor de x ≥ 0; além disso, pode definir x2/(3√x) em todo valor de x ≠ 0. Então faça x > 0 e invoque o teorema §59-4 sobre um quociente de funções.

Tente obter esse resultado só com a definição de derivada, isto é, sem recorrer a nenhum dos teoremas §59-1 a §59-6; veja de quanto trabalho os teoremas te poupam.
§60-15. Se f(x) = senx, ache f’(x).
Resolução. Bem, pode definir f em todo valor de x. Para achar a derivada de senx em x = x, faça ϖ um infinitésimo positivo ou negativo:

Na seção 25 (parte d’A extraordinária linha dos números hiper-reais), viu que st[(senϖ)/ϖ] = 1. Quanto a (cosϖ – 1)/ϖ, deve ser um infinitésimo; veja como conduzir uma prova por contradição.
Presuma que (cosϖ – 1)/ϖ não é um infinitésimo; logo, é um hiper-real infinito. E quanto ao produto a seguir?

Sendo o produto de dois infinitos, deve ser um infinito. Contudo, pode trocar cos2ϖ por 1 – sen2ϖ. Veja o que acontece:
![]()
Essa expressão está infinitamente próxima de –1, o que contradiz sua pressuposição inicial. Logo, (cosϖ – 1)/ϖ não é um hiper-real infinito, mas um infinitésimo, e está infinitamente próximo de zero. Assim, continuando:

No gráfico a seguir, você pode acompanhar a dança entre a função senx e sua derivada, cosx. Veja como cosx = 0 nos pontos em que senx atinge um máximo ou um mínimo; veja como cosx é negativo quando o valor de senx está diminuindo, e como cosx é positivo quando o valor de senx está aumentando. Nesta dança entre senx e cosx, está muito do que você precisa saber sobre a arte de pegar uma função derivada e examiná-la para descobrir informações sobre a função original.

Uma das muitas plotagens de sen(x) e de cos(x) que pode achar na internet
§60-16. Se f(x) = cosx, ache f’(x).
Resolução. Pode definir f para todo valor de x. Além disso:

Veja abaixo a dança entre cosx (em preto) e –senx (em vermelho); especialmente, veja que –senx = 0 quando cosx atinge um máximo ou um mínimo.

§60-17. Se f(x) = tanx, ache f’(x).
Resolução. Bem, tanx = senx/cosx. Logo, você pode definir f sempre que cosx ≠ 0, isto é, sempre que x ≠ kπ/2, com k inteiro ímpar. Se fizer isso, daí basta recorrer à regra da derivada de um quociente de funções (teorema §59-4) e ao resultado dos dois problemas anteriores.

Pode usar qualquer uma das três expressões da última linha como derivada de tanx. Na plotagem a seguir, a função tanx está em preto, e sua derivada sec²x em vermelho.

§60-18. Se f(x) = secx, ache f’(x).
Resolução. Mais uma vez, secx = 1/cosx; portanto, só pode definir f quando x ≠ kπ/2, com k inteiro ímpar. Bem, faça x ≠ kπ/2 e invoque a regra pela qual calcula a derivada do recíproco de uma função (teorema §59-3).

§60-19. Se f(x) = cotx, ache f’(x).
Resolução. Agora, cotx = cosx/senx. Sabe que senx = 0 quando x = kπ, com k inteiro. Logo, faça x ≠ kπ e invoque a regra da derivada de um quociente de funções.

§60-20. Se f(x) = cscx, ache f’(x).
Resolução. Bem, cscx é a mesma coisa que cosecx, e ambos são iguais a 1/senx. Portanto, pode definir a função f sempre que senx ≠ 0, isto é, sempre que x ≠ kπ, com k inteiro; fazendo assim, invoque a regra da derivada do recíproco de uma função (§59-3).

§60-21. Se f(x) = senx2, ache f’(x).
Resolução. Faça y = h(x) = x2 e f(x) = g(y) = seny. Daí pode definir f para todo valor de x, e, sendo assim, tudo o que tem a fazer é invocar a regra da cadeia (teorema §59-5).

No gráfico abaixo, veja a dança entre senx² (em preto) e de sua derivada 2xcosx² (em vermelho). Em palavras: quanto maior o valor de x, maior a magnitude da taxa instantânea de mudança de senx², pois mais velozmente a função senx² oscila. Esse é um jeito de explicar por que o engenheiro, quando quer obrigar algum mecanismo a oscilar muito velozmente, tem de fornecer bastante energia ao mecanismo.

§60-22. Diferencie (x + 3)2.
Resolução. “Diferencie” significa “ache a função derivada da função que tem em mãos” ou “ache uma expressão adequada para o coeficiente diferencial”. Bem, pode definir (x + 3)2 para todo valor de x; se fizer f(x) = x2 e g(x) = x + 3, daí f(g(x)) = (x + 3)2, e com isso invoque uma vez mais a regra da cadeia.

Caso queira, pode expandir a expressão (x + 3)2 e diferenciar o polinômio x2 + 6x + 9 termo a termo.

§60-23. Diferencie √(x2 + 7).
Resolução. Faça g(x) = √x e h(x) = x2 + 7. Daí f(x) = g(h(x)) = √(x2 + 7). Pode definir f para todo valor de x, já que o argumento da raiz nunca é negativo, isto é, x2 + 7 ≥ 7 para todo valor de x. Para achar a derivada de f, use a regra da cadeia e o que já descobriu no problema §60-8.

Tanto pode usar o resultado da terceira linha quanto o da quinta linha, que é a expressão na terceira linha com o divisor “racionalizado”. Alguns professores ainda pedem ao aluno que “racionalize o divisor”, o que só faz sentido se o aluno pretende realizar contas à mão. Contudo, todo mundo usa calculadoras e computadores, e com frequência é mais fácil teclar a expressão não racionalizada na calculadora do que a expressão racionalizada. Além disso, se você fizer x = π, o divisor π2 + 7 é um número irracional, exatamente o que se quer evitar ao racionalizar o divisor… Em livros mais recentes, cada vez mais autores deixam as expressões como a da terceira linha — exceto se a expressão racionalizada for mais bonita, como é o caso do problema a seguir.
§60-24. Diferencie 1/√x.
Resolução. Em primeiro lugar, só pode definir 1/√x para x > 0. Use mais uma vez o resultado do problema §60-8 e a regra da derivada do recíproco de uma função (teorema §59-3). Eis o que deve obter:

A expressão na última linha parece mesmo mais bonita que as expressões nas linhas anteriores.
§60-25. Calcule [√x]’, mas desta vez use a regra da cadeia; faça g(x) = x2.
Resolução. Faça, como o redator recomendou, g(x) = x2. Faça também f(x) = √x; não se esqueça de que f, a função na qual está interessado, só vale para x ≥ 0, visto que está trabalhando apenas com números reais. E por fim faça h(x) = g(f(x)) = (√x)2 = x. Já sabe que h’(x) = 1. Veja como pode prosseguir:

Note que a expressão para f’ só vale quando x > 0. Isso não significa dizer que não existe uma reta tangente a f quando x = 0, porque ela existe: é a linha reta vertical x = 0, isto é, é o próprio eixo das ordenadas. Ambas compartilham o ponto (0, 0).

§60-26. Prove que f(x) = |x| é contínua em x = 0.
Resolução. Antes de mais nada, ponha no papel, com mais detalhes, o que significa a função f.

Logo, f(0) = 0. Bem, f é contínua em zero se, e somente se, 0 ≈ ϖ implica f(0) ≈ f(ϖ) para todo infinitésimo ϖ, positivo ou negativo. Se ϖ é positivo, f(ϖ) = ϖ ≈ 0 = f(0); e, se ϖ é negativo, f(ϖ) = –ϖ ≈ 0 = f(0). Assim, em qualquer um dos dois casos, para todo hiper-real ϖ infinitamente próximo de zero, f(0) está infinitamente próximo de f(ϖ), e portanto f é contínua em zero.

§60-27. Prove que, embora f(x) = |x| seja contínua em x = 0, não pode diferenciá-la em x = 0.
Resolução. Para todo infinitésimo positivo ϖ:
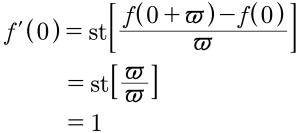
Da mesma forma, para todo infinitésimo negativo ϖ:

Sendo assim, você não pode dizer que f é diferenciável em zero, pois, embora 𝕯f(0)/𝕯x seja um hiper-real finito não importa qual infinitésimo ϖ você escolha, o valor padrão de 𝕯f(0)/𝕯x varia conforme a escolha de ϖ.
Sutileza. Se quiser, diga que f(x) = |x| é diferenciável no intervalo (–∞, 0], assim como no intervalo [0, ∞). Pois f’(x) = –1 para todo x no intervalo (–∞, 0) e, além disso, f’(0) = –1 para todo infinitésimo ϖ negativo (f é derivável à esquerda de zero). Da mesma forma, f’(x) = 1 para todo x no intervalo (0, ∞) e, além disso, f’(0) = 1 para todo infinitésimo ϖ positivo (f é derivável à direita de zero). Apesar disso, visto que f não é diferenciável em x = 0, diga que f é diferenciável em todo x ≠ 0.
§63-1. Estude a função f(x) = x|x|. (a) Prove que, para x > 0, f’(x) = 2x. (b) Prove que, para x < 0, f’(x) = –2x. (c) Prove que f’(0) = 0.
Resolução. Se x > 0, f(x) = x2. Use a regra da derivada de uma potência inteira de x (teorema §59-6) e faça a conta de cabeça: f’(x) = 2x. Se x < 0, f(x) = –x2, e f’(x) = –2x. E se x = 0?
Estude primeiro o caso com um infinitésimo ϖ > 0.

E agora o caso com um infinitésimo ϖ < 0.

Visto que f’(0) = 0 para qualquer infinitésimo ϖ, positivo ou negativo, diga que f é diferenciável em zero. Eis como resumir o que sabe sobre f e f’ numa expressão só:

Note que f’(x) nunca é negativo; isso quer dizer que f nunca é decrescente. (Você não deve dizer que f é sempre crescente, pois em x = 0 a função não cresce nem decresce, e por isso sua derivada vale zero. O certo é mesmo dizer que f nunca é decrescente, por mais esquisito que isso pareça para quem gosta de escrever com ousadia.)
A aparência de x|x|
§61-1. Prove que [rx–n]’ = –nrx–n–1.
Resolução. Veja como talvez fiquem suas notas.

Em palavras: a regra da derivada de uma potência de x vale para expoentes inteiros negativos.
§63-2. Prove que não pode derivar f(x) = 2|x| em x = 0.
Resolução. Como já viu no problema §60-7, se f(x) = 2|x|, daí f’(x) = 2[|x|]’; e, como já viu no problema §60-27, não pode diferenciar |x| quando x = 0.
§63-3. Se h(x) = f(x)g(x) é uma função infinitamente diferenciável, parta do teorema §59-2 e proponha uma expressão para h(n)(x).
Resolução. A certa altura de suas notas, deve ter sentido a necessidade de adotar notação nova, para ajudá-lo a ver o que estava acontecendo e para evitar dezenas de xis entre parênteses. Adote, portanto, a seguinte notação:

Assim, f0 significa que você não derivou a função f nenhuma vez; f5 significa que a derivou cinco vezes. (Isto é, tirou a derivada de f, a derivada da derivada, a derivada da derivada da derivada, etc.)
Eis como devem ficar suas notas ao fazer as contas para as primeiras cinco derivadas de h:

Talvez tenha notado várias coincidências nessas linhas. Eis uma lista incompleta:
(1) A expressão para h0 tem uma parcela; a expressão para h1 tem duas parcelas; a expressão para h2 tem três parcelas; a expressão para h4 tem cinco parcelas; e a expressão para h5 tem seis parcelas. Suponha, portanto, que a expressão para hn deve ter n + 1 parcelas.
(2) O coeficiente da parcela na expressão para h0 está na linha zero do triângulo de Pascal. (Veja a figura logo abaixo.) Os coeficientes das duas parcelas na expressão para h1 estão na linha 1. Os coeficientes das três parcelas na expressão para h2 estão na linha 2. Os coeficientes das quatro parcelas na expressão para h3 estão na linha 3. Os coeficientes das cinco parcelas na expressão para h4 estão na linha 4. Os coeficientes das seis parcelas na expressão para h5 estão na linha 5. Suponha então que os coeficientes das n + 1 parcelas na expressão para hn estão na linha n do triângulo de Pascal.

Lembrete. Os termos na enésima linha do triângulo de Pascal são os coeficientes binomiais a seguir, nos quais r = 0, 1, 2, 3, …, n.

(3) Os índices superescritos de f e de g vão de n a 0 no caso de f e de 0 a n no caso de g. Assim, presuma que, no caso de hn, a enésima derivada de h, você vai trabalhar com fng0, fn–1g1, fn–2g2, …, f1gn–1, f0gn.
Com tudo isso, já pode pôr no papel sua conjectura de como calcular a enésima derivada de h.

Agora, deve provar que sua conjectura é válida para todo n inteiro não negativo; recorra ao princípio da indução matemática. Como primeiro passo, prove que é válida quando n = 0.

Ela é válida, pois partiu do pressuposto de que h(x) = f(x)g(x).
Agora vem o passo indutivo. Deve provar que, se a conjectura é válida quando n = k, então também é válida quando n = k + 1 (com k inteiro não negativo). Assim, ponha a conjectura no papel quando n = k.

Tire a derivada de hk.

Bem, pela regra da derivada de um produto de funções, cada parcela vai se transformar em duas parcelas. Nas linhas a seguir, pode ver as duplas dispostas em duas colunas, o que mais tarde vai tornar o pensamento mais fácil.

Note que pode adicionar os coeficientes dos termos cujos índices superescritos são os mesmos. Assim:

Pausa: como pode achar uma expressão para representar a soma C(n, r–1) + C(n, r)? [Lembrete: C(n, r) é outro jeito de denotar um número binomial.] Use a definição e as propriedades do fatorial.

Sendo assim, ao realizar todas as adições de coeficientes binomiais, vai ficar com a equação a seguir.

Quase lá! Só falta agora acertar o primeiro coeficiente e o último. Use as duas igualdades a seguir; se quiser, faça as contas para ver como realmente são iguais para todo valor inteiro não negativo de k.

Use essa descoberta na expressão para hk+1.

Essa é exatamente a expressão que escreveria para hk+1 se tivesse recorrido à conjectura logo duma vez. Assim, recapitulando, a conjectura é válida para n = 0. Visto que, sendo ela válida para n = k, é também válida para n = k + 1, pode concluir que é válida para n = 1, 2, 3, 4, 5, etc. Tem agora o direito de chamá-la de teorema. Vale a pena colocá-lo no papel com notação convencional:
Teorema. Se h(x) = f(x)g(x) é uma função que pode diferenciar quantas vezes bem entender, então deve calcular a enésima derivada de h com a fórmula a seguir.

Observação: Se um dia quiser provar o teorema binomial, pode usar o argumento acima com algumas modificações.
§63-4. Você tem diante de si o gráfico da parábola y = f(x) = ax2 + bx + c, expressão na qual a, b, c são coeficientes reais, com a ≠ 0. Como pode produzir a fórmula com a qual calcular as coordenadas do vértice da parábola?
Resolução. No vértice da parábola, f’(x) = 0; pois, pelo teorema do valor médio, tem de existir um ponto no qual a derivada vale zero; é o que sugere a figura a seguir.

Crédito: Claudio Rocchini, Wikipedia.
Calcule a derivada de f de cabeça, se quiser, recorrendo à regra da derivada de parcelas com expoentes inteiros de x, e depois a iguale a zero.

Com tal expressão, confirma algo que já sabia: a parábola tem um único vértice, pois a expressão para x quando f’(x) = 0 só pode assumir um valor. E qual é o valor de y = f(x) quando x = –b/(2a)?

Assim, as coordenadas do vértice da parábola y = f(x) = ax2 + bx + c são:

Veja como é fácil realizar tais contas com um pouco de cálculo diferencial. Nunca mais precisará decorar a fórmula das coordenadas do vértice de uma parábola, se é que algum dia decorou.
§63-5. Em várias das demonstrações até aqui, você pensou num intervalo aberto (a, b), e destacou um número c desse intervalo. Para algum infinitésimo ϖ, positivo ou negativo, explique mais uma vez por que c + ϖ faz parte do intervalo.
Resolução. É por causa do teorema §23-1, que viu na matéria sobre continuidade: Faça a < b dois números reais. Daí, se p é qualquer hiper-real no intervalo (a, b), então st[p] também é. Se fizer p = c + ϖ para algum infinitésimo ϖ, positivo ou negativo, responde completamente à pergunta §63-5.
§63-6. Presuma que a função f(x) = logx está bem definida e tem uma função derivada f’(x). Como poderia provar que f’(x) = k/x para alguma constante k?
Resolução. Presuma que f’(1) = k. É uma pressuposição razoável, pois a função f deve ter alguma inclinação em x = 1. Daí, para todo b > 0:

Note que f(b) = logb é um valor constante, pois b não é uma variável, e sim um valor fixo. Use a regra da cadeia para diferenciar a equação acima.

Faça agora x = 1.

Usará essa informação nas próximas matérias desta série, especialmente para construir a constante e. A pergunta §63-6 é a versão moderna de uma pergunta que vários matemáticos fizeram a si mesmos nos séculos 17 e 18, inclusive Euler.
§63-7. Considere a função a seguir:

(a) Prove que f é descontínua para todo x ≠ 0. (b) Prove, contudo, que f é diferenciável em x = 0.
Resolução. Se x ≠ 0 é irracional, sempre pode escolher um infinitésimo ϖ de modo que x + ϖ seja racional. Pois sempre pode fazer isso com números reais; por exemplo, se adiciona 2 – √2 ao número irracional √2, obtém a soma racional 2. Pelo teorema de Łós, se pode fazer isso com reais, pode fazer isso com hiper-reais também. Veja o que acontece, portanto, se x ≠ 0 é irracional, mas escolhe ϖ de modo que x + ϖ é racional.

Neste caso, portanto, f’(x) não existe, pois (2x2)/ϖ é um hiper-real infinito. Agora, se x ≠ 0 é irracional, também pode escolher um infinitésimo ϖ de modo que x + ϖ continue sendo irracional. Veja daí como fica a derivada f’(x):

Uma história semelhante acontece quando x ≠ 0 é racional, mas x + ϖ é irracional [f’(x) não existe], e quando x ≠ 0 e x + ϖ são ambos racionais [f’(x) = 2x].
Em outras palavras, para todo valor de x ≠ 0, o valor de f’(x) se alterna entre existente e não existente conforme você muda o valor do infinitésimo ϖ, e por isso diga que não pode diferenciar f em nenhum valor de x ≠ 0.
E quando x = 0?

Assim, pode diferenciar f num único ponto: x = 0. Não é incrível que, com um novo sistema de números (o sistema dos hiper-reais), e com as ferramentas intelectuais do cálculo, possa descobrir uma coisa dessas?
No gráfico a seguir, veja em preto a plotagem de f para x racional, e em vermelho a plotagem de f para x irracional.

§67-1. Verifique se x2 e √y são funções inversas.
Resolução. Tudo o que deve fazer é criar duas expressões: y = f(x) = x2 e x = g(y) = y(1/2). Daí verifique as duas igualdades a seguir: f(g(y)) = y e g(f(x)) = x. É simples, em tese, mas deve explorar esse problema um pouco mais.
Se y = f(x) = x2, f’(x) = 2x. Logo, f’(x) > 0 para todo x > 0, e você pode aplicar o teorema da função inversa (corolário §66-1).

Isso é uma equação diferencial; é uma espécie de pergunta: “Qual é a função g(y), onde y = f(x) = x2, tal que g’(y) seja 1/(2x) para todo x > 0?” Numa situação de pesquisa, você teria de procurar uma função com tais características; mas o redator do enunciado deu a dica.
Se g(y) = √y, daí, visto que y = x2, g(x2) = √(x2) = |x|; mas, como está lidando com x > 0, |x| = x. Logo, g’(y) = [x]’ = 1. Veja o que obtém ao aplicar o teorema da função inversa e a regra da cadeia na mesma sequência de deduções.

Então, visto que g(y) = √y cumpre corretamente seu papel à luz do corolário §66-1, y = f(x) = x2 e g(y) = √y são funções inversas para todo x > 0.
Use um argumento semelhante a esse para x < 0, e deve trabalhar com g’(y) = [|x|]’ = –1, como já viu no problema §60-27. Quando x = 0, não tem como recorrer ao corolário para descobrir as características de f e de g, pois não pode dividir nada por zero. Mas, visto que x2 = 0 somente se x = 0, e como f’(x) = 0 somente se x = 0 (f’ não tem nenhum outro zero), se quiser pode construir uma função inversa g mais parruda: para x ≥ 0, g(y) = √y = |x| = x; ou então, para x ≤ 0, g(y) = –√y = –|x|.
Como vê, estudar as inter-relações entre uma função e sua inversa exige quebrar a cabeça de verdade; não é à toa que, muitas vezes, o aluno de ensino médio antipatiza com esse assunto.

§67-2. Verifique se 2x – 5 e (1/2)(y + 5) são funções inversas.
Resolução. Talvez tenha notado que isso é bem simples: se faz y = f(x) = 2x – 5, daí, ao adicionar 5 aos dois lados da equação, e ao dividir os dois lados por 2, fica com x = g(y) = (1/2)(y + 5).
Pode agora verificar a validade do teorema da função inversa: f é diferenciável e f’(x) = 2 > 0 para todo x real. Afinal, f é uma reta no plano. Logo, f tem uma função inversa g, definida para todo valor de f(x), e para todo y = f(x) vale a afirmação a seguir.

O corolário §66-1 é o que matemáticos chamam de “argumento de existência”. Com ele, você sabe que, se f é diferenciável em (a, b), e se f’(x) > 0 ou f’(x) < 0 em (a, b), então f tem uma função inversa g (ela existe), e você pode saber bem depressa qual é a derivada de g nesse intervalo. Às vezes, f e g têm uma relação tão complicada que saber isso já é saber bastante.
§67-3. Verifique se 10x e log10y são funções inversas.
Resolução. Por definição, y = f(x) = 10x se, e somente se, x = g(y) = log10y. Se quisesse, poderia parar a resposta aqui.
Agora, qual é o valor de g’(y), de acordo com o teorema da função inversa? Para saber isso, primeiro calcule o valor de f’(x).

Por enquanto não tem ferramentas teóricas para calcular o valor padrão da expressão entre colchetes (em breve terá); use, portanto, uma boa calculadora científica.

Caso acredite na calculadora, portanto, o valor de g’(y) é:

Note que, para quem sabe muito pouco sobre o comportamento de f e de g, até que, graças aos teoremas, você sabe bastante.
§67-4. Verifique se xn e y(1/n) são funções inversas.
Resolução. Suponha primeiro que n ≠ 0 é um inteiro positivo. Você já sabe que xn é diferenciável, pois é uma função polinomial; sabe também que [xn]’ = nx^(n – 1). Se n é par, a derivada [xn]’ é maior ou igual a zero para todo x maior ou igual a zero, e ela só tem um zero quando x = 0; se n é ímpar, a derivada é maior ou igual a zero para todo valor de x, e ela só tem um zero quando x = 0. Daí:

Portanto, f e g são funções inversas uma da outra.
Para ser preciso: se n é par, x = n√y ou x = –n√y, e deve escolher um desses dois casos; por exemplo, x = g(y) = n√y. Se n é ímpar, não precisa se preocupar com nenhuma restrição a g.
O caso em que n ≠ 0 é negativo é semelhante a esse, embora a plotagem das curvas fique bem diferente, como pode ver a seguir com x² (preto), x³ (vermelho), 1/x² (azul), e 1/x³ (verde).

§67-5. Ache a inversa de x + 7.
Resolução. Fácil: se y = f(x) = x + 7, daí x = y – 7. Portanto, x = g(y) = y – 7. Pode verificar como f(g(y)) = y e g(f(x)) = x. Como sabe que sua expressão para g é verdadeira em qualquer valor de x? Sabe disso porque f’(x) = 1 > 0 para todo valor de x.
§67-6. Ache a inversa de 3x – 1.
Resolução. Direto ao ponto:

§67-7. Ache a inversa de x3.
Resolução. Com um pouco mais de detalhes desta vez.
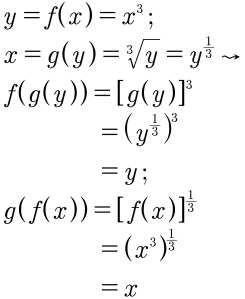
Em palavras: você parte de f, acha a função inversa g, e verifica se f(g(y)) = y e se g(f(x)) = x. Ao estudar o perfil de f’, a derivada de f, você na verdade estuda o perfil do domínio e do contradomínio de f e de sua função inversa g. Neste caso, veja o gráfico abaixo, com f em preto e f’ em vermelho: visto que f’ é estritamente decrescente quando x < 0, estritamente crescente quando x > 0, e que só tem um zero quando x = 0, sabe que f tem uma função inversa g para todo valor de x.

§67-8. Ache a inversa de x√x.
Resolução. Esse é mais difícil, então vale a pena acompanhar uma resolução mais detalhada.
Se y = f(x) = x√x, de imediato sabe que x ≥ 0, pois só pode definir √x se x ≥ 0. Calcule agora a derivada de f.

Sendo assim, f’(x) > 0 para todo x > 0. Note que não pode dizer “f’(x) ≥ 0 para todo x ≥ 0”, pois não pode calcular f’(0). Essa ressalva é muito importante. Pois a expressão arrumadinha na terceira linha do formulário acima é apenas uma expressão equivalente à da segunda linha, que é a verdadeira função derivada f’ e contém √x num divisor. Bem, se f’(x) > 0 para todo x > 0, f é estritamente crescente no intervalo (0, ∞), e portanto tem uma função inversa g nesse intervalo. Ela é:

Agora verifique se f(g(y)) = y e g(f(x)) = x.

Então, OK, f e g são funções inversas uma da outra. Contudo, embora não possa definir f’(x) quando x = 0, pode definir tanto f quanto g, pois zero faz parte do domínio de f e f(x) = 0 só quando x = 0; em outras palavras, f não tem nenhum outro zero. Sendo assim, se quiser denotar f e g mais completamente, escreva:

No gráfico a seguir, pode ver f em preto e g em vermelho.

§67-9. Use o problema §67-4 para provar que a derivada de g(y) = y(1/n) é g’(y) = (1/n)y(1/n)–1.
Resolução. Basta aplicar o teorema da função inversa, e não se esqueça de que x = y(1/n).

Note que, uma vez feita a descoberta, é irrelevante se escreve x = y(1/n) ou y = x(1/n). Sendo assim, anote mais esta regra de derivação:

Ao usar a regra, não se esqueça de refletir sobre restrições: n ≠ 0 e, para usar a fórmula de f’(x), x ≠ 0 caso n ≥ 1. Mais uma vez: isso não significa que não existe reta tangente a f em x = 0; significa apenas que deve achar a tangente por outros meios.
§67-10. Use o problema §67-9 e os teoremas §59-5 e §59-6 para provar que a derivada de xn/m é (n/m)x(n/m)–1.
Resolução. Faça y = f(x) = xn e g(y) = y(1/m), com m ≠ 0. Faça daí h(x) = g(f(x)) = (xn)(1/m) = x(n/m). Use a regra da cadeia e a regra da derivada de uma potência inteira de x.

Muitos se referem a essa regra como “a regra da derivada de uma potência racional de x”, da qual a regra da derivada de uma potência inteira de x é um caso especial. (Esse movimento é comum entre matemáticos: você usa uma afirmação específica para provar uma mais genérica, da qual a afirmação específica passa a ser um caso especial.) Se quiser, verifique a validade da expressão a seguir, na qual r é um número real qualquer.

§67-11. Ache um intervalo no qual existe a função inversa de senx, e calcule a derivada de sen–1y.
Resolução. Bem, y = f(x) = senx é diferenciável para todo x, e a derivada f’(x) = cosx é maior que zero no intervalo (–π/2) < x < (π/2); portanto, pelo teorema da função inversa, senx tem uma função inversa no intervalo aberto (–π/2, π/2). Examine a curva de y = senx na figura a seguir. No intervalo fechado [–π/2, π/2], o valor de senx não se repete nenhuma vez, pois sen(–π/2) = –1, sen(π/2) = 1, e senx é estritamente crescente no intervalo aberto (–π/2, π/2); portanto, se quiser diga que senx tem uma função inversa no intervalo fechado [–π/2, π/2].

Logo, veja como definir a função inversa de senx e sua derivada.
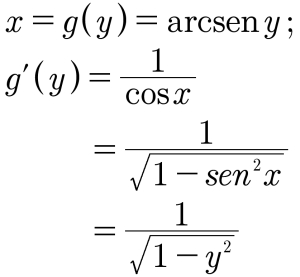
Note que embora possa definir a função g no intervalo fechado [–π/2, π/2], só deve definir a função derivada g’ no intervalo aberto (–π/2, π/2), pois tem de evitar zero no divisor.
Agora, se apresentar as funções g e g’ a seu leitor do jeito que estão, ele talvez as ache esquisitas, pois parece que x e y trocaram de lugar. (E trocaram.) Para corrigir isso, primeiro apresente ao leitor as fórmulas com x e y nos lugares em que normalmente aparecem: y é a variável dependente, x é a independente.
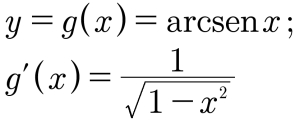
Mas dê um aviso mais ou menos assim: “Na primeira expressão acima, x é um número real do intervalo fechado [–1, 1], e y é um número do intervalo [–π/2, π/2]; na segunda expressão, x é um número do intervalo aberto (–1, 1), para que não aconteça de ter zero no divisor.”
Note, contudo, que existem infinitos valores de y tais que seny = x, pois a função seno é periódica. Assim, se y = arcsenx, daí seny = x, mas também no mínimo sen(y + 2π) = x, sen(y + 4π) = x, etc.

Crédito: Geek3, Wikipedia.
Lembrete: arcseny = sen–1y.
§67-12. Ache um intervalo no qual existe a função inversa de tanx, e calcule a derivada de tan–1y.
Resolução. Bem, só de olhar o gráfico de y = f(x) = tanx você pode ver que a derivada f’(x) = 1 + tan2x é estritamente positiva no intervalo aberto (–π/2, π/2). Logo, pode construir a inversa de f nesse intervalo, se quiser.

Se faz x = g(y) = arctany, com y real e x ∈ (–π/2, π/2), daí:

Mais uma vez, y = tanx é uma função periódica. Se entra com o valor de y numa calculadora científica e ela devolve um valor de x no intervalo (–π/2, π/2), saiba que existem infinitos outros valores de x tais que y = tanx.
Lembrete: arctany = tan–1y.
{70}/ Uma sutileza sobre a notação
No texto anterior desta série, você viu que pode definir a integral de f no intervalo [a, b] com a expressão a seguir, na qual usou dx para denotar um infinitésimo positivo.

Contudo, quando estudou a definição de derivada nesta parte da série, não usou dx para denotar um infinitésimo, e sim ϖ. Por quê? Veja mais uma vez a expressão a seguir:

Perceba que tem usado dy/dx para denotar um número real, e fez isso para combinar com a tradição. Se usasse dx dentro dos colchetes, para denotar um hiper-real infinitésimo, não poderia usá-lo fora dos colchetes na expressão dy/dx para denotar a derivada de f em b. E daí também não poderia escrever, como é muito natural, f’(x) = dy/dx.
Na análise padrão, a situação é quase a mesma, pois tem de usar dy/dx para denotar um limite, que é o limite de [f(b + h) – f(b)]/h quando h tende a zero, sendo h uma variável real positiva ou negativa. Então, mais uma vez, para deixar esse ponto bem claro: ao escrever dy/dx, não quer dizer o quociente do infinitésimo dy pelo infinitésimo dx; antes, quer dizer a parte real do quociente do infinitésimo 𝕯f pelo infinitésimo 𝕯x, isto é, dy/dx = st[𝕯f/𝕯x].

{71}/ Cuidado com relações indevidas de causa e efeito
No começo deste texto, você supôs que certa magnitude y crescia ou diminuía em função de certa magnitude x; e examinou o exemplo do forno, cuja temperatura y cresce em função do tempo x. Ao longo das seções 56 a 70, descobriu que pode usar dy/dx ou f’(x) para denotar a velocidade instantânea com que a temperatura y subia no tempo x = x.
Cuidado! Não se deixe levar pelos significados corriqueiros da palavra “função” e da locução “em função de”; pois talvez atribua relação de causa e efeito a duas magnitudes que não têm nenhuma relação de causa e efeito. A temperatura do forno não sobe porque o tempo passa. Ela sobe por causa de uma quantidade imensa de motivos: o gás está fluindo normalmente e está queimando, há oxigênio suficiente no ar para o gás continuar queimando, não há vazamentos de calor no forno, não há dentro do forno nenhum dispositivo que retira calor do ar, etc. Por um acaso conveniente, a temperatura sobe e o cronômetro funciona, de modo que o homem registra os dois fenômenos num gráfico, com a temperatura no eixo Y e o tempo no eixo X, emprega a linguagem y = f(x), e com isso ganha toda a teoria que tais iniciativas, matematicamente, implicam.
Em algumas faculdades na Rússia, o professor pede aos alunos que pronunciem a expressão y = f(x) com palavras mais ou menos assim: “y é correspondência de x”. Isso quer dizer: “Com f, para cada valor de x, faço corresponder um e só um valor de y.” Esse uso é tão comum entre estudantes de matemática que o matemático russo Edward Frenkel, quando se mudou para os Estados Unidos, ficou surpreso com os americanos: eles usavam a palavra “correspondência” para dizer “troca de cartas, bilhetes, e-mails”. {FIM}
Aviso. Caso veja algum erro neste capítulo ou queira tirar uma dúvida, escreva para o redator:
<ImaginarioPuro.MarcioSimoes@gmail.com>.












 Aviso 3: Para escrever este curso, usei como referência o ótimo livrinho Infinitesimal Calculus, de James M. Henle e Eugene M. Kleinberg, ambos matemáticos americanos. (Usei a edição da Dover de 2003.) No entanto, este curso não é uma tradução do livro de Henle & Kleinberg: às vezes, fico “perto” do que os dois professores americanos escreveram, mas outras vezes me afasto bastante. Se lê inglês, eis meu conselho: compre o livro de Henle & Kleinberg e o estude com atenção duas ou três vezes, com intervalo de uns poucos meses entre cada vez. Você não vai se arrepender.
Aviso 3: Para escrever este curso, usei como referência o ótimo livrinho Infinitesimal Calculus, de James M. Henle e Eugene M. Kleinberg, ambos matemáticos americanos. (Usei a edição da Dover de 2003.) No entanto, este curso não é uma tradução do livro de Henle & Kleinberg: às vezes, fico “perto” do que os dois professores americanos escreveram, mas outras vezes me afasto bastante. Se lê inglês, eis meu conselho: compre o livro de Henle & Kleinberg e o estude com atenção duas ou três vezes, com intervalo de uns poucos meses entre cada vez. Você não vai se arrepender.