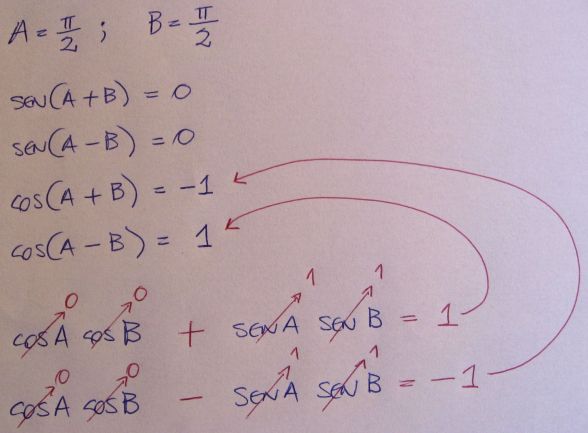Um estudante (vou chamá-lo de QaC) sempre se esquece da regra pela qual expandir sen(A + B), sen(A – B), cos(A + B), cos(A – B), expressões nas quais QaC usa A e B para denotar ângulos medidos em radianos. Ele até se lembra de uma musiquinha que ouviu uma vez num cursinho pré-vestibular:
“Minha tenha tem palmeiras, onde canta o sabiá: seno A, cosseno B, seno B, cosseno A.”
Ele também lembra que deve montar duas das quatro expansões com cosseno A, cosseno B, seno A, seno B (isto é, em duas delas não deve misturar senos e cossenos); e deve montar duas delas com seno A, cosseno B, seno B, cosseno A (em duas delas, deve misturar senos e cossenos). Mas QaC raramente recorda qual expressão se refere a qual soma.
Portanto, QaC deve aplicar a musiquinha a qual expressão? E qual sinal deve usar: + ou –? Em outras palavras, a musiquinha fala de senA cosB + senB cosA ou de senA cosB – senB cosA?
Essas expansões são importantes, pois aparecem a todo momento na matemática pura e na aplicada. Por exemplo, quando QaC estava interessado em descobrir o porquê da regra pela qual deve dividir um número complexo por outro, viu que ela surge naturalmente de uma expressão do tipo cos(θ + ϕ).
Mas, mais uma vez, para QaC recordar o a expansão de cos(θ + ϕ), teve de consultar uma tabela no dicionário de matemática. Recentemente, contudo, atinou com um método.
Como primeiro passo, desenhou um versão bem simples do círculo trigonométrico, o círculo de raio igual a 1 (figura 1). Com ele, é fácil ver que cos(0) = 1, cos(π) = (–1), sen(π/2) = 1, sen(–π/2) = (–1). [Ou, na linguagem mais usada no ensino básico, cos(0º) = 1, cos(180º) = (–1), sen(90º) = 1, sen(–90º) = (–1).] E depois pensou assim: “Em primeiro lugar, tenho de escolher dois ângulos A e B que produzam sen(A + B) = 1 e sen(A – B) = (–1), ou vice-versa; ou então que produzam cos(A + B) = 1 e cos(A – B) = (–1), ou vice-versa.”
Figura 1: O círculo trigonométrico
Começou com A = 0 e B = π/2. Daí sen(A + B) = 1, sen(A – B) = (–1), cos(A + B) = 0, cos(A – B) = 0. Escreveu as possibilidades no caderno, mas colocou um quadradinho no lugar em que deveria colocar mais tarde ou o sinal de mais ou o sinal de menos:
senA cosB ☐ senB cosA
senA cosB ☐ senB cosA
cosA cosB ☐ senA senB
cosA cosB ☐ senA senB
Bem, se A = 0 e B = π/2, daí QaC simplesmente olhou a figura 1 para ver que senA = 0, senB = 1, cosA = 1, cosB = 0. Com essas informações, a lista fica ficou assim:
(senA cosB = 0) ☐ (senB cosA = 1)
(senA cosB = 0) ☐ (senB cosA = 1)
(cosA cosB = 0) ☐ (senA senB = 0)
(cosA cosB = 0) ☐ (senA senB = 0)
Nesse ponto, QaC achou fácil ver que as duas primeiras fórmulas se referem a sen(A + B) e sen(A – B); as duas últimas se referem a cos(A + B) e cos(A – B). Além disso, viu que, se colocasse o sinal de mais na primeira, ela teria de se referir a sen(A + B); e se colocasse o sinal de menos na segunda, ela teria de se referir a sen(A – B):
sen(A + B) = senA cosB + senB cosA
sen(A – B) = senA cosB – senB cosA
Bem, QaC viu que metade do trabalho estava pronto, e desta vez não teve de recorrer a nenhuma musiquinha, nem teve de olhar a tabela de identidades trigonométricas no dicionário de matemática.
Depois, para produzir dois cossenos opostos, QaC escolheu A = π/2 e B = π/2. Com isso, cos(A + B) = (–1) e cos(A – B) = 1. Além disso:
(cosA cosB = 0) ☐ (senA senB = 1)
(cosA cosB = 0) ☐ (senA senB = 1)
Achou fácil ver que deveria colocar o sinal de mais na primeira expressão, e o sinal de menos na segunda, para produzir o que queria.
cosA cosB + senA senB = 1
cosA cosB – senA senB = (–1)
Portanto, a primeira expressão se refere a cos(A – B) = 1 e a segunda, a cos(A + B) = (–1). Daí QaC escreveu as duas linhas que faltavam:
cos(A + B) = cosA cosB – senA senB
cos(A – B) = cosA cosB + senA senB
Depois disso, repetiu o método duas vezes, para se familiarizar com ele, e percebeu que, se precisasse dessas igualdades numa emergência, saberia repetir o procedimento para produzir as quatro igualdades sem nenhum erro. {FIM}
Um jeito de montar a tabela com canetas de duas cores
Círculo trigonométrico. Você também pode chamá-lo de “círculo unitário”. É muito útil. Pode imaginá-lo num plano cartesiano, com o centro na origem. Daí um ponto P no círculo determina um arco de comprimento equivalente ao número real x. [A medida desse comprimento é positiva se você a medir no sentido anti-horário, do ponto (1, 0) ao ponto P, e negativa se a medir no sentido horário.] Com a projeção ortogonal de P no eixo das abscissas, você vê o comprimento equivalente a cosx. Com a projeção ortogonal de P no eixo das ordenadas, vê o comprimento equivalente a senx. Com esse círculo, pode ver claramente por que sen(π/2) = 1 e cos(π/2) = 0, por exemplo, assim como pode ver por que –1 ≤ cosx ≤ 1, ou por que sen²x + cos²x = 1, entre muitas outras propriedades de senos e cossenos.
{Imaginário Puro} 